如果你也在 怎样代写流体力学Fluid Mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
流体力学是物理学的一个分支,涉及流体(液体、气体和等离子体)的力学和对它们的力。它的应用范围很广,包括机械、土木工程、化学和生物医学工程、地球物理学、海洋学、气象学、天体物理学和生物学。
statistics-lab™ 为您的留学生涯保驾护航 在代写流体力学Fluid Mechanics方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写流体力学Fluid Mechanics代写方面经验极为丰富,各种代写流体力学Fluid Mechanics相关的作业也就用不着说。
我们提供的流体力学Fluid Mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
物理代写|流体力学代写Fluid Mechanics代考|Properties of Fluids, Continuum Hypothesis
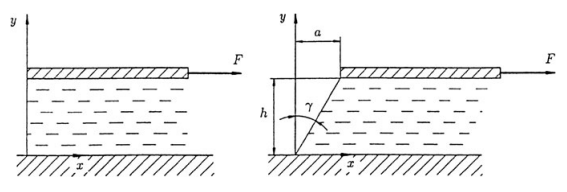
Fluid mechanics is concerned with the behavior of materials which deform without limit under the influence of shearing forces. Even a very small shearing force will deform a fluid body, but the velocity of the deformation will be correspondingly small. This property serves as the definition of a fluid: the shearing forces necessary to deform a fluid body go to zero as the velocity of deformation tends to zero. On the contrary, the behavior of a solid body is such that the deformation itself, not the velocity of deformation, goes to zero when the forces necessary to deform it tend to zero. To illustrate this contrasting behavior, consider a material between two parallel plates and adhering to them acted on by a shearing force $F$ (Fig. 1.1).
If the extent of the material in the direction normal to the plane of Fig. 1.1 and in the $x$-direction is much larger than that in the $y$-direction, experience shows that for many solids (Hooke’s solids), the force per unit area $\tau=F / A$ is proportional to the displacement $a$ and inversely proportional to the distance between the plates $h$. At least one dimensional quantity typical for the material must enter this relation, and here this is the shear modulus $G$. The relationship
$$
\tau=G \gamma(\gamma \ll 1)
$$
between the shearing angle $\gamma=a / h$ and $\tau$ satisfies the definition of a solid: the force per unit area $\tau$ tends to zero only when the deformation $\gamma$ itself goes to zero. Often the relation for a solid body is of a more general form, e.g., $\tau=f(\gamma)$, with $f(0)=0$.
If the material is a fluid, the displacement of the plate increases continually with time under a constant shearing force. This means there is no relationship between the displacement, or deformation, and the force. Experience shows here that with many fluids the force is proportional to the rate of change of the displacement, that is, to the velocity of the deformation. Again the force is inversely proportional to the distance between the plates. (We assume that the plate is being dragged at
constant speed, so that the inertia of the material does not come into play.) The dimensional quantity required is the shear viscosity $\eta$, and the relationship with $U=\mathrm{d} a / \mathrm{d} t$ now reads
$$
\tau=\eta \frac{U}{h}=\eta \dot{\gamma},
$$
or, if the shear rate $\dot{\gamma}$ is set equal to $\mathrm{d} u / \mathrm{d} y$.
$$
\tau(y)=\eta \frac{\mathrm{d} u}{\mathrm{~d} y} .
$$
$\tau(y)$ is the shêar streess on a surfacee eelement parallèl to the plates at point $y$. In so-called simple shearing flow (rectilinear shearing flow) only the $x$-component of the velocity is nonzero, and is a linear function of $y$.
The above relationship was known to Newton, and it is sometimes incorrectly used as the definition of a Newtonian fluid: there are also non-Newtonian fluids which show a linear relationship between the shear stress $\tau$ and the shear rate $\dot{\gamma}$ in this simple state of stress. In general, the relationship for a fluid reads $\tau=f(\dot{\gamma})$, with $f(0)=0$.
While there are many substances for which this classification criterion suffices, there are some which show dual character. These include the glasslike materials which do not have a crystal structure and are structurally liquids. Under prolonged loads these substances begin to flow, that is to deform without limit. Under short-term loads, they exhibit the behavior of a solid body. Asphalt is an oftquoted example: you can walk on asphalt without leaving footprints (short-term load), but if you remain standing on it for a long time, you will finally sink in. Under very short-term loads, e.g., a blow with a hammer, asphalt splinters, revealing its structural relationship to glass. Other materials behave like solids even in the long-term, provided they are kept below a certain shear stress, and then above this stress they will behave like liquids. A typical example of these substances (Bingham materials) is paint: it is this behavior which enables a coat of paint to stick to surfaces parallel to the force of gravity.
物理代写|流体力学代写Fluid Mechanics代考|The behavior of solids
The behavior of solids, liquids and gases described up to now can be explained by the molecular structure, by the thermal motion of the molecules, and by the interactions between the molecules. Microscopically the main difference between gases on the one hand, and liquids and solids on the other is the mean distance between the molecules.
With gases, the spacing at standard temperature and pressure $(273.2 \mathrm{~K}$; $1.013$ bar) is about ten effective molecular diameters. Apart from occasional collisions, the molecules move along a straight path. Only during the collision of, as a rule, two molecules, does an interaction take place. The molecules first attract each other weakly, and then as the interval between them becomes noticeably smaller than the effective diameter, they repel strongly. The mean free path is in general larger than the mean distance, and can occasionally be considerably larger.
With liquids and solids the mean distance is about one effective molecular diameter. In this case there is always an interaction between the molecules. The large resistance which liquids and solids show to volume changes is explained by the repulsive force between molecules when the spacing becomes noticeably smaller than their effective diameter. Even gases have a resistance to change in volume, although at standard temperature and pressure it is much smaller and is proportional to the kinetic energy of the molecules. When the gas is compressed so far that the spacing is comparable to that in a liquid, the resistance to volume change becomes large, for the same reason as referred to above.
Real solids show a crystal structure: the molecules are arranged in a lattice and vibrate about their equilibrium position. Above the melting point, this lattice disintegrates and the material becomes liquid. Now the molecules are still more or less ordered, and continue to carry out their oscillatory motions although they often exchange places. The high mobility of the molecules explains why it is easy to deform liquids with shearing forces.
It would appear obvious to describe the motion of the material by integrating the equations of motion for the molecules of which it consists: for computational reasons this procedure is impossible since in general the number of molecules in the material is very large. But it is impossible in principle anyway, since the position and momentum of a molecule cannot be simultaneously known (Heisenberg’s Uncertainty Principle) and thus the initial conditions for the integration do not exist. $\mathrm{~ I n ~ a ̊ d d i t i o ̄ n , ~ d e t a ̄ i l e ̉ ~ i n f o r m a ̄ t i o n ̃ ~ a b o o u t ~ t h e ~ m o ̄ l e ́ c u l a}$ and therefore it would be necessary to average the molecular properties of the motion in some suitable way. It is therefore far more appropriate to consider the average properties of a cluster of molecules right from the start.
物理代写|流体力学代写Fluid Mechanics代考|On the other hand the linear measure of the volume
On the other hand the linear measure of the volume must be small compared to the macroscopic length of interest. It is appropriate to assume that the volume of the fluid particle is infinitely small compared to the whole volume occupied by the fluid. This assumption forms the basis of the continuum hypothesis. Under this hypothesis we consider the fluid particle to be a material point and the density (or other properties) of the fluid to be continuous functions of place and time. Occasionally we will have to relax this assumption on certain curves or surfaces, since discontinuities in the density or temperature, say, may occur in the context of some idealizations. The part of the fluid under observation consists then of infinitely many material points, and we expect that the motion of this continuum will be described by partial differential equations. However the assumptions which have led us from the material to the idealized model of the continuum are not always fulfilled. One example is the flow past a space craft at very high altitudes, where the air density is very low. The number of molecules required to do any useful averaging then takes up such a large volume that it is comparable to the volume of the craft itself.
Continuum theory is also inadequate to describe the structure of a shock (see Chap. 9), a frequent occurrence in compressible flow. Shocks have thicknesses of the same order of magnitude as the mean free path, so that the linear measures of the volumes required for averaging are comparable to the thickness of the shock.
We have not yet considered the role the thermal motion of molecules plays in the continuum model. This thermal motion is reflected in the macroscopic properties of the material and is the single source of viscosity in gases. Even if the macroscopic velocity given by (1.4) is zero, the molecular velocities $\vec{c}{i}$ are clearly not necessarily zero. The consequence of this is that the molecules migrate out of the fluid particle and are replaced by molecules drifting in. This exchange process gives rise to the macroscopic fluid properties called transport properties. Obviously, molecules with other molecular properties (e.g. mass) are brought into the fluid particle. Take as an example a gas which consists of two types of molecule, say $\mathrm{O}{2}$ and $\mathrm{N}{2}$. Let the number of $\mathrm{O}{2}$ molecules per unit volume in the fluid particle be larger than that of the surroundings. The number of $\mathrm{O}_{2}$ molecules which migrate out is proportional to the number density inside the fluid particle, while the number which drift in is proportional to that of the surroundings. The net effect is that more $\mathrm{O}{2}$ molecules drift in than drift out and so the $\mathrm{O}{2}$ number density adjusts itself to the surroundings. From the standpoint of continuum theory the process described above represents the diffusion.
流体力学代写
物理代写|流体力学代写Fluid Mechanics代考|Properties of Fluids, Continuum Hypothesis
流体力学研究材料在剪切力的影响下无限制地变形的行为。即使是非常小的剪切力也会使流体变形,但变形的速度会相应地很小。此属性用作流体的定义:当变形速度趋于零时,使流体变形所需的剪切力变为零。相反,实体的行为是,当使其变形所需的力趋于零时,变形本身而不是变形速度会趋于零。为了说明这种对比行为,考虑两个平行板之间的材料并通过剪切力作用在它们上F(图 1.1)。
如果材料在垂直于图 1.1 平面的方向上的范围和在X- 方向远大于是-方向,经验表明,对于许多固体(胡克固体),单位面积的力τ=F/一个与位移成正比一个并且与板之间的距离成反比H. 材料的至少一维量必须进入这个关系,这里是剪切模量G. 关系
τ=GC(C≪1)
剪切角之间C=一个/H和τ满足固体的定义:单位面积的力τ仅在变形时趋于零C本身归零。通常,实体的关系具有更一般的形式,例如,τ=F(C), 和F(0)=0.
如果材料是流体,则在恒定剪切力下,板的位移随时间不断增加。这意味着位移或变形与力之间没有关系。这里的经验表明,对于许多流体,力与位移的变化率成正比,即与变形的速度成正比。同样,力与板之间的距离成反比。(我们假设盘子被拖到
恒定速度,使材料的惯性不会发挥作用。)所需的尺寸量是剪切粘度这,以及与的关系在=d一个/d吨现在读
τ=这在H=这C˙,
或者,如果剪切速率C˙设置为等于d在/d是.
τ(是)=这d在 d是.
τ(是)是表面元素上的剪切应力,平行于点的板是. 在所谓的简单剪切流(直线剪切流)中,只有X-速度的分量是非零的,并且是一个线性函数是.
上面的关系是牛顿所知道的,它有时被错误地用作牛顿流体的定义:也有非牛顿流体显示出剪切应力之间的线性关系τ和剪切速率C˙在这种简单的压力状态下。一般来说,流体的关系读取τ=F(C˙), 和F(0)=0.
虽然有许多物质可以满足这一分类标准,但也有一些物质表现出双重特征。这些包括不具有晶体结构并且在结构上为液体的玻璃状材料。在长时间的负载下,这些物质开始流动,即无限变形。在短期载荷下,它们表现出实体的行为。沥青是一个经常被引用的例子:你可以在沥青上行走而不留下脚印(短期负荷),但如果你长时间站在上面,你最终会陷入。在非常短期的负荷下,例如,一击用锤子,沥青碎裂,揭示了它与玻璃的结构关系。其他材料即使在长期内也表现得像固体,只要它们保持在一定的剪切应力以下,然后超过这个应力,它们就会表现得像液体。
物理代写|流体力学代写Fluid Mechanics代考|The behavior of solids
到目前为止所描述的固体、液体和气体的行为可以通过分子结构、分子的热运动以及分子之间的相互作用来解释。从微观上看,一方面是气体,另一方面是液体和固体之间的主要区别是分子之间的平均距离。
对于气体,在标准温度和压力下的间距(273.2 ķ; 1.013bar) 约为十个有效分子直径。除了偶尔的碰撞外,分子沿着笔直的路径移动。通常,只有在两个分子发生碰撞时,才会发生相互作用。分子首先相互弱吸引,然后随着它们之间的间隔变得明显小于有效直径,它们强烈排斥。平均自由程通常大于平均距离,有时可能会大得多。
对于液体和固体,平均距离约为一个有效分子直径。在这种情况下,分子之间总是存在相互作用。当间距明显小于它们的有效直径时,液体和固体对体积变化表现出的大阻力可以通过分子之间的排斥力来解释。甚至气体也对体积变化有抵抗力,尽管在标准温度和压力下它要小得多并且与分子的动能成正比。当气体被压缩到与液体相当的程度时,由于与上述相同的原因,对体积变化的阻力变大。
真实的固体显示出晶体结构:分子排列成晶格并围绕它们的平衡位置振动。高于熔点,这种晶格会分解,材料变成液体。现在分子或多或少还是有序的,尽管它们经常交换位置,但它们仍继续进行振荡运动。分子的高流动性解释了为什么用剪切力很容易使液体变形。
很明显,通过对构成材料的分子的运动方程进行积分来描述材料的运动是显而易见的:由于计算原因,这个过程是不可能的,因为通常材料中的分子数量非常大。但无论如何原则上是不可能的,因为不能同时知道分子的位置和动量(海森堡的不确定性原理),因此积分的初始条件不存在。̉ 我n 一个̊dd一世吨一世○̄n, d和吨一个̄一世l和̉ 一世nF○r米一个̄吨一世○ñ 一个b○○在吨 吨H和 米○̄l和́C在l一个因此,有必要以某种合适的方式平均运动的分子特性。因此,从一开始就考虑分子簇的平均特性更为合适。
物理代写|流体力学代写Fluid Mechanics代考|On the other hand the linear measure of the volume
另一方面,与感兴趣的宏观长度相比,体积的线性度量必须很小。假设流体粒子的体积与流体占据的整个体积相比无限小是合适的。这个假设构成了连续统假设的基础。在这个假设下,我们认为流体粒子是一个质点,流体的密度(或其他性质)是位置和时间的连续函数。有时我们将不得不放宽对某些曲线或曲面的这一假设,因为密度或温度的不连续性可能发生在某些理想化的背景下。被观察的流体部分由无限多的质点组成,我们期望这个连续体的运动可以用偏微分方程来描述。然而,将我们从材料引向理想化的连续统模型的假设并不总是得到满足。一个例子是在非常高的高度流过一艘航天器,那里的空气密度非常低。进行任何有用的平均所需的分子数量然后占据如此大的体积,以至于它与工艺本身的体积相当。
连续介质理论也不足以描述冲击的结构(见第 9 章),这是可压缩流动中经常发生的情况。冲击的厚度与平均自由程的数量级相同,因此平均所需体积的线性测量值与冲击的厚度相当。
我们还没有考虑分子的热运动在连续体模型中所起的作用。这种热运动反映在材料的宏观性质中,并且是气体粘度的单一来源。即使(1.4)给出的宏观速度为零,分子速度C→一世显然不一定为零。其结果是分子从流体粒子中迁移出来并被漂移进来的分子所取代。这种交换过程产生了称为传输特性的宏观流体特性。显然,具有其他分子特性(例如质量)的分子被带入流体粒子中。以一种由两种分子组成的气体为例,比如说○2和ñ2. 让数○2流体颗粒中每单位体积的分子大于周围的分子。的数量○2迁移出去的分子与流体粒子内部的数量密度成正比,而流入的分子数量与周围环境的数量成正比。净效果是更多○2分子漂移进来而不是漂移出去,所以○2数字密度会根据周围环境进行自我调整。从连续统理论的角度来看,上述过程代表了扩散。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
