如果你也在 怎样代写商业分析Statistical Modelling for Business这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
商业分析就是利用数据分析和统计的方法,来分析企业之前的商业表现,从而通过分析结果来对未来的商业战略进行预测和指导 。
statistics-lab™ 为您的留学生涯保驾护航 在代写商业分析Statistical Modelling for Business方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写商业分析Statistical Modelling for Business方面经验极为丰富,各种代写商业分析Statistical Modelling for Business相关的作业也就用不着说。
我们提供的商业分析Statistical Modelling for Business及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等楖率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
统计代写|商业分析作业代写Statistical Modelling for Business代考|Optional
The statistical analyst’s goal should be to present the most accurate and truthful portrayal of a data set that is possible. Such a presentation allows managers using the analysis to make informed decisions. However, it is possible to construct statistical summaries that are misleading. Although we do not advocate using misleading statistics, you should be aware of some of the ways statistical graphs and charts can be manipulated in order to distort the truth. By knowing what to look for, you can avoid being misled by a (we hope) small number of unscrupulous practitioners.
As an example, suppose that the nurses at a large hospital will soon vote on a proposal to join a union. Both the union organizers and the hospital administration plan to distribute recent salary statistics to the entire nursing staff. Suppose that the mean nurses’ salary at the hospital and the mean nurses’ salary increase at the hospital (expressed as a percentage) for each of the last four years are as follows:
The hospital administration does not want the nurses to unionize and, therefore, hopes to convince the nurses that substantial progress has been made to increase salaries without a union. On the other hand, the union organizers wish to portray the salary increases as minimal so that the nurses will feel the need to unionize.
Figure $2.29$ gives two bar charts of the mean nurses’ salaries at the hospital for each of the last four years. Notice that in Figure $2.29$ (a) the administration has started the vertical scale of the bar chart at a salary of $\$ 58,000$ by using a scale break ( ). Alternatively, the chart
could be set up without the scale break by simply starting the vertical scale at $\$ 58,000$. Starting the vertical scale at a value far above zero makes the salary increases look more dramatic. Notice that when the union organizers present the bar chart in Figure $2.29$ (b), which has a vertical scale starting at zero, the salary increases look far less impressive.
Figure $2.30$ presents two bar charts of the mean nurses’ salary increases (in percentages) at the hospital for each of the last four years. In Figure $2.30$ (a), the administration has made the widths of the bars representing the percentage increases proportional to their heights. This makes the upward movement in the mean salary increases look more dramatic because the observer’s eye tends to compare the areas of the bars, while the improvements in the mean salary increases are really only proportional to the heights of the bars. When the union organizers present the bar chart of Figure $2.30$ (b), the improvements in the mean salary increases look less impressive because each bar has the same width.
Figure $2.31$ gives two time series plots of the mean nurses’ salary increases at the hospital for the last four years. In Figure $2.31$ (a) the administration has stretched the vertical axis of the graph. That is, the vertical axis is set up so that the distances between the percentages are large. This makes the upward trend of the mean salary increases appear to be steep. In Figure $2.31$ (b) the union organizers have compressed the vertical axis (that is, the distances between the percentages are small). This makes the upward trend of the
mean salary increases appear to be gradual. As we will see in the exercises, stretching and compressing the horizontal axis in a time series plot can also greatly affect the impression given by the plot.
It is also possible to create totally different interpretations of the same statistical summary by simply using different labeling or captions. For example, consider the bar chart of mean nurses’ salary increases in Figure 2.30(b). To create a favorable interpretation, the hospital administration might use the caption “Salary Increase Is Higher for the Fourth Year in a Row.” On the other hand, the union organizers might create a negative impression by using the caption “Salary Increase Fails to Reach $10 \%$ for Fourth Straight Year.”
In summary, it is important to carefully study any statistical summary so that you will not be misled. Look for manipulations such as stretched or compressed axes on graphs, axes that do not begin at zero, bar charts with bars of varying widths, and biased captions. Doing these things will help you to see the truth and to make well-informed decisions.
统计代写|商业分析作业代写Statistical Modelling for Business代考|Descriptive Analytics
In Section $1.5$ we said that descriptive analytics uses traditional and more recently developed graphics to present to executives (and sometimes customers) easy-to-understand visual summaries of up-to-the-minute information conceming the operational status of a business. In this section we will discuss some of the more recently developed graphics used by descriptive analytics, which include gauges, bullet graphs, treemaps, and sparklines. In addition, we will see how they are used with each other and more traditional graphics to form analytic dashboards, which are part of executive information systems. We will also briefly discuss data discovery, which involves, in it simplest form, data drill down.
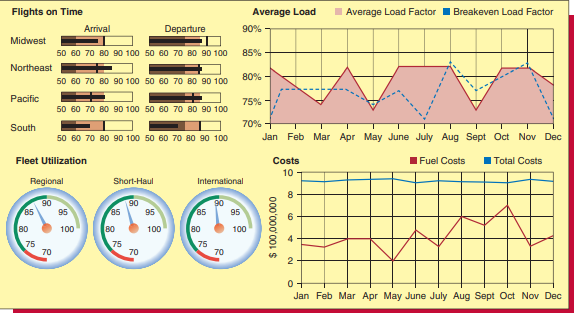
Dashboards and gauges An analytic dashboard provides a graphical presentation of the current status and historical trends of a business’s key performance indicators. The term dashboard originates from the automotive dashboard, which helps a driver monitor a car’s key functions. Figure $2.35$ shows a dashboard that graphically portrays some key performance indicators for a (fictitious) airline for last year. In the lower left-hand portion of the dashboard we see three gauges depicting the percentage utilizations of the regional, short-haul, and international fleets of the airline. In general, a gauge (chart) allows us to visualize data in a way that is similar to a real-life speedometer needle on an automobile. The outer scale of the gauge is often color coded to provide additional performance information. For example, note that the colors on the outer scale of the gauges in Figure $2.35$ range from red to dark green to light green. These colors signify percentage fleet utilizations that range from poor (less than 75 percent) to satisfactory (less than 90 percent but at least 75 percent) to good (at least 90 percent).
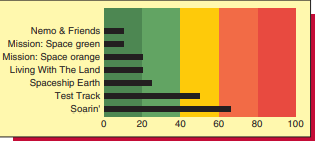
Bullet graphs While gauge charts are nice looking, they take up considerable space and to some extent are cluttered. For example, recalling the Disney Parks Case, using seven $\mathrm{~ ส ม ่ ม ด ร ~ c h a}$ seven Epcot rides would take up considerable space and would be less efficient than using the bullet graph that we originally showed in Figure 1.8. That bullet graph (which has been obtained using Excel) is shown again in Figure 2.36.
In general, a bullet graph features a single measure (for example, predicted waiting time) and displays it as a horizontal bar (or a vertical bar) that extends into ranges representing qualitative measures of performance, such as poor, satisfactory, and good. The ranges are displayed as either different colors or as varying intensities of a single hue. Using a single hue makes them discernible by those who are color blind and restricts the use of color if the bullet graph is part of a dashboard that we don’t want to look too “busy.” Many bullet graphs compare the single primary measure to a target, or objective, which is represented by a symbol on the bullet graph. The bullet graph of Disney’s predicted waiting times uses five colors ranging from dark green to red and signifying short ( 0 to 20 minutes) to very long ( 80 to 100 minutes) predicted waiting times. This bullet graph does not compare the predicted waiting times to an objective. However, the bullel graphs located in the upper left of the dashboard in Figure $2.35$ (representing the percentages of on-time arrivals and departures for the airline) do display obbjectives represented by shoort vertical black lines. For examplé, consider the bullet graphs representing the percentages of on-time arrivals and departures in the Midwest, which are shown below.
统计代写|商业分析作业代写Statistical Modelling for Business代考|sparkline
Sparklines Figure $2.38$ shows sparklines depicting the monthly closing prices of five stocks over six months. In general, a sparkline, another of the new descriptive analytics graphics, is a line chart that presents the general shape of the variation (usually over time) in some measurement, such as temperature or a stock price. A sparkline is typically drawn without axes or coordinates and made small enough to be embedded in text. Sparklines are often grouped together so that comparative variations can be seen. Whereas most charts are designed to show considerable information and are set off from the main text, sparklines are intended to be succinct and located where they are discussed. Therefore, if the sparklines in Figure $2.38$ were located in the text of a report comparing stocks, they would probably be made smaller than shown in Figure $2.38$, and the actual monthly closing prices of the stocks used to obtain the sparklines would probably not be shown next to the sparklines.
Data discovery To conclude this section, we briefly discuss data discovery methods, which allow decision makers to interactively view data and make preliminary analyses. One simple version of data discovery is data drill down, which reveals more detailed data that underlie a higher-level summary. For example, an online presentation of the airline dashboard in Figure $2.35$ might allow airline executives to drill down by clicking the gauge which shows that approximately 89 percent of the airline’s international fleet was utilized over the year to see the bar chart in Figure 2.39. This bar chart depicts the quarterly percentage utilizations of the airline’s international fleet over the year. The bar chart suggests that the airline might offer international travel specials in quarter 1 (Winter) and quarter 4 (Fall) to increase international travel and thus increase the percentage of the international fleet utilized in those quarters. Drill down can be done at multiple levels. For example, Disney executives might wish to have weekly reports of total merchandise sales at its four Orlando parks, which can be drilled down to reveal total merchandise sales at each park, which can be further drilled down to reveal total merchandise sales at each “land” in each park, which can be yet further drilled down to reveal total merchandise sales in each store in each land in each park.
金融中的随机方法代写
统计代写|商业分析作业代写Statistical Modelling for Business代考|Optional
统计分析师的目标应该是尽可能准确和真实地描述数据集。这样的演示允许管理人员使用分析来做出明智的决定。但是,有可能构建具有误导性的统计摘要。虽然我们不提倡使用误导性统计数据,但您应该了解一些统计图表可能被操纵以歪曲事实的方式。通过知道要寻找什么,您可以避免被(我们希望)少数不道德的从业者误导。
例如,假设一家大型医院的护士很快将对加入工会的提案进行投票。工会组织者和医院管理部门都计划向全体护理人员分发最近的工资统计数据。假设过去四年每年在医院的平均护士工资和在医院的平均护士工资增长(以百分比表示)如下:
医院管理部门不希望护士加入工会,因此希望让护士相信,在没有工会的情况下提高工资已经取得了实质性进展。另一方面,工会组织者希望将工资增长描述为最低限度,以便护士感到有必要加入工会。
数字2.29给出过去四年中每年医院护士平均工资的两个条形图。请注意,在图2.29(a) 行政部门已开始以条形图的垂直刻度为$58,000通过使用比例分隔符 ( )。或者,图表
可以通过简单地在$58,000. 从远高于零的值开始垂直刻度会使工资增长看起来更加显着。请注意,当工会组织者呈现图2.29(b),垂直尺度从零开始,工资增长看起来远没有那么令人印象深刻。
数字2.30显示了过去四年每年医院护士平均工资增长(百分比)的两个条形图。如图2.30(a),政府已使代表百分比增加的条形的宽度与其高度成正比。这使得平均工资增长的向上运动看起来更加显着,因为观察者的眼睛倾向于比较条形的区域,而平均工资增长的改善实际上只与条形的高度成正比。当工会组织者呈现图的条形图2.30(b),平均工资增长的改善看起来不那么令人印象深刻,因为每个条具有相同的宽度。
数字2.31给出了过去四年医院平均护士工资增长的两个时间序列图. 如图2.31(a) 行政当局拉长了图表的纵轴。即,纵轴被设置为使得百分比之间的距离大。这使得平均工资增长的上升趋势显得陡峭。如图2.31(b) 工会组织者压缩了纵轴(即百分比之间的距离很小)。这使得上涨趋势
平均工资增长似乎是渐进的。正如我们将在练习中看到的那样,在时间序列图中拉伸和压缩水平轴也会极大地影响该图给人的印象。
也可以通过简单地使用不同的标签或标题来创建对相同统计摘要的完全不同的解释。例如,考虑图 2.30(b) 中护士平均工资增长的条形图。为了创造一个有利的解释,医院管理部门可能会使用“工资增长连续第四年更高”的标题。另一方面,工会组织者可能会通过使用标题“加薪未能达到”来制造负面印象10%连续第四年。”
总之,重要的是仔细研究任何统计摘要,以免被误导。寻找操作,例如图形上的拉伸或压缩轴、不从零开始的轴、具有不同宽度条形的条形图以及有偏差的标题。做这些事情将帮助你看清真相并做出明智的决定。
统计代写|商业分析作业代写Statistical Modelling for Business代考|Descriptive Analytics
在部分1.5我们说过,描述性分析使用传统的和最近开发的图形向高管(有时是客户)呈现易于理解的关于企业运营状态的最新信息的视觉摘要。在本节中,我们将讨论描述性分析使用的一些最近开发的图形,包括仪表、子弹图、树状图和迷你图。此外,我们将看到它们如何相互使用,以及如何使用更传统的图形来形成分析仪表板,这些仪表板是执行信息系统的一部分。我们还将简要讨论数据发现,它以最简单的形式涉及数据钻取。
仪表板和仪表 分析仪表板提供企业关键绩效指标的当前状态和历史趋势的图形表示。仪表板一词源于汽车仪表板,它可以帮助驾驶员监控汽车的关键功能。数字2.35显示了一个仪表板,该仪表板以图形方式描绘了一家(虚构的)航空公司去年的一些关键绩效指标。在仪表板的左下角,我们看到三个仪表,描述了航空公司的区域、短途和国际机队的利用率百分比。一般来说,仪表(图表)允许我们以类似于现实生活中汽车上的速度表指针的方式可视化数据。仪表的外部刻度通常采用颜色编码,以提供额外的性能信息。例如,请注意图中仪表外部刻度上的颜色2.35范围从红色到深绿色到浅绿色。这些颜色表示从差(低于 75%)到满意(低于 90% 但至少 75%)到好(至少 90%)的车队利用率百分比。
子弹图 虽然仪表图看起来很漂亮,但它们占用了相当大的空间,并且在某种程度上显得杂乱无章。例如,回顾迪斯尼公园案例,使用七个สม่มดร 小号米的米dR CH一种七次 Epcot 游乐设施将占用相当大的空间,并且效率低于我们最初在图 1.8 中显示的子弹图。图 2.36 再次显示了该项目符号图(已使用 Excel 获得)。
通常,项目符号图具有单个度量(例如,预测的等待时间)并将其显示为水平条(或垂直条),该条延伸到表示性能定性度量的范围,例如差、满意和良好。范围显示为不同的颜色或单一色调的不同强度。如果项目符号图是我们不想看起来太“忙碌”的仪表板的一部分,则使用单一色调可以让色盲者识别它们并限制颜色的使用。许多子弹图将单个主要度量与目标或目标进行比较,目标或目标由子弹图上的符号表示。迪士尼预计等待时间的子弹图使用从深绿色到红色的五种颜色,表示预计等待时间短(0 到 20 分钟)到非常长(80 到 100 分钟)。此项目符号图未将预测的等待时间与目标进行比较。但是,位于图2.35(代表航空公司准时到达和离开的百分比)确实显示了由短的垂直黑线表示的目标。例如,考虑代表中西部准时到达和离开百分比的子弹图,如下所示。
统计代写|商业分析作业代写Statistical Modelling for Business代考|sparkline
迷你图2.38显示了描述 5 只股票在 6 个月内的月收盘价的迷你图。一般来说,迷你图是另一种新的描述性分析图形,是一种折线图,它显示了某些测量(例如温度或股票价格)中变化的一般形状(通常随时间变化)。迷你图通常在没有轴或坐标的情况下绘制,并且足够小以嵌入文本中。迷你图通常组合在一起,以便可以看到比较变化。尽管大多数图表旨在显示大量信息并与正文分开,但迷你图旨在简洁并位于讨论它们的位置。因此,如果图中的迷你图2.38位于比较股票的报告的文本中,它们可能会比图所示的更小2.38,用于获取迷你图的股票的实际每月收盘价可能不会显示在迷你图旁边。
数据发现 为了结束本节,我们将简要讨论数据发现方法,这些方法允许决策者以交互方式查看数据并进行初步分析。数据发现的一个简单版本是数据钻取,它揭示了更详细的数据,这些数据是更高级别摘要的基础。例如,图 1 中航空公司仪表板的在线演示2.35可能允许航空公司管理人员通过单击显示该航空公司国际机队的大约 89% 在一年中被使用的仪表进行深入研究,以查看图 2.39 中的条形图。此条形图描绘了该航空公司国际机队在一年中的季度利用率百分比。条形图表明航空公司可能会在第 1 季度(冬季)和第 4 季度(秋季)提供国际旅行特价,以增加国际旅行,从而增加这些季度使用的国际机队的百分比。下钻可以在多个级别进行。例如,迪斯尼高管可能希望每周报告其奥兰多四个公园的商品总销售额,可以深入了解每个公园的商品总销售额,
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。统计代写|python代写代考
随机过程代考
在概率论概念中,随机过程是随机变量的集合。 若一随机系统的样本点是随机函数,则称此函数为样本函数,这一随机系统全部样本函数的集合是一个随机过程。 实际应用中,样本函数的一般定义在时间域或者空间域。 随机过程的实例如股票和汇率的波动、语音信号、视频信号、体温的变化,随机运动如布朗运动、随机徘徊等等。
贝叶斯方法代考
贝叶斯统计概念及数据分析表示使用概率陈述回答有关未知参数的研究问题以及统计范式。后验分布包括关于参数的先验分布,和基于观测数据提供关于参数的信息似然模型。根据选择的先验分布和似然模型,后验分布可以解析或近似,例如,马尔科夫链蒙特卡罗 (MCMC) 方法之一。贝叶斯统计概念及数据分析使用后验分布来形成模型参数的各种摘要,包括点估计,如后验平均值、中位数、百分位数和称为可信区间的区间估计。此外,所有关于模型参数的统计检验都可以表示为基于估计后验分布的概率报表。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
statistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
机器学习代写
随着AI的大潮到来,Machine Learning逐渐成为一个新的学习热点。同时与传统CS相比,Machine Learning在其他领域也有着广泛的应用,因此这门学科成为不仅折磨CS专业同学的“小恶魔”,也是折磨生物、化学、统计等其他学科留学生的“大魔王”。学习Machine learning的一大绊脚石在于使用语言众多,跨学科范围广,所以学习起来尤其困难。但是不管你在学习Machine Learning时遇到任何难题,StudyGate专业导师团队都能为你轻松解决。
多元统计分析代考
基础数据: $N$ 个样本, $P$ 个变量数的单样本,组成的横列的数据表
变量定性: 分类和顺序;变量定量:数值
数学公式的角度分为: 因变量与自变量
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
