如果你也在 怎样代写复杂网络complex networks这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
复杂网络是由数量巨大的节点和节点之间错综复杂的关系共同构成的网络结构。
statistics-lab™ 为您的留学生涯保驾护航 在代写复杂网络complex networks方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写复杂网络complex networks方面经验极为丰富,各种代写复杂网络complex networks相关的作业也就用不着说。
我们提供的复杂网络complex networks及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等楖率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
统计代写|复杂网络代写complex networks代考|Patterns of Link Structure
The above discussion has shown the importance of investigating the link structure in real world networks. One can view this problem as a kind of pattern detection. Patterns are generally viewed as expressions of some kind of regularity. What such a regularity may be, however, remains often a vague concept. It might be sensible to define everything as regular which is not random.
The structure this monograph is concerned with is a particular type of non-random structure in complex networks which is closely related to the aforementioned correlations. The section about correlations has shown that if the different types of nodes in a network are known, the link structure of the network may show a particular signature. In the majority of cases, however, the presence of different types of nodes is only hypothesized and the type of each node is unknown. The purpose of this work is to develop methods to detect the presence of different types of nodes in networks and to find the putative type of each node. A number of possible applications from various fields shall motivate the problem again.
Suppose we are given a communication network of an enterprise. Nodes are employees and links represent communication, e.g., via e-mail, between them. We may then search for “communities of practice” – employees who are particularly well connected among each other, i.e., with highly enriched in-group communication. It is then possible to compare these communities of practice to the organizational structure of the enterprise and possibly use the results in the assembly of teams for future projects. A study in this direction has been performed by Tyler et al. [26].
Novel experimental techniques from biology allow the automatic extraction of all proteins produced by an organism. Proteins are the central building blocks of biological function, but generally, proteins do not function alone but bind to one another to form complexes which in turn are capable of performing a particular function, such as initiating the transcription of a particular piece of DNA. It is now possible to study the pairwise binding interactions of a large number of proteins in an automated way $[27]$. The result of such a study is a protein interaction network in which the links represent pairwise interactions between proteins. Protein function should be mirrored in such a network. For instance, proteins forming part of a complex should now be detectable as densely interlinked groups of nodes in such a network [28]. An analysis of the structure of a protein interaction or other biological network
created by automated experiments hence presents a first step in planning future experiments [29].
The collection of scientific articles represent a strongly fragmented repository of scientific knowledge $[30,31]$. Online databases make it possible to study these in an automated way, e.g., in form of co-authorship networks or citation networks. In the former, nodes are researchers while links represent co-authorship of one or more articles. Analysis of the structure of this network may give valuable information about the cooperation between various scientists and aid in the evaluation of funding policy or influence future funding decisions. In the latter, nodes in the network are scientific articles and links denote the citation of one from the other. Analysis of the structure of this network may yield insight into the different research areas of a particular field of science.
统计代写|复杂网络代写complex networks代考|Positions, Roles and Equivalences
By investigating data from a wide range of sources encompassing the life sciences, ecology, information and social sciences as well as economics, researchers have shown that an intimate relation between the topology of a network and the function of the nodes in that network indeed exists [1-9]. A central idea is that nodes with a similar pattern of connectivity will perform a similar function. Understanding the topology of a network will be a first step in understanding the function of individual nodes and eventually the dynamics of any network.
As before, we can base our analysis on the work done in the social sciences. In the context of social networks, the idea that the pattern of connectivity is related to the function of an agent in the network is known as playing a “role” or assuming a “position” $[10,11]$. Here, we will endorse this idea.
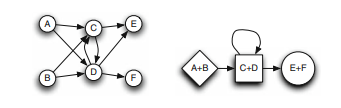
The nodes in a network may be grouped into equivalence classes according to the role they play. Two basic concepts have been developed to formalize the assignments of roles individuals play in social networks: structural and regular equivalence. Both are illustrated in Fig. 2.1. Two nodes are called structurally equivalent if they have the exact same neighbors [12]. This means that in the adjacency matrix of the network, the rows and columns of the corresponding nodes are exactly equal. The idea behind this type of equivalence is that two nodes which have the exact same interaction partners can only perform the exact same function in the network. In Fig. 2.1, only nodes $A$ and $B$ are structurally equivalent while all other nodes are structurally equivalent only to themselves.
To relax this very strict criterion, regular equivalence was introduced [13, 14]. Two nodes are regularly equivalent if they are connected in the same way to equivalent others. Clearly, all nodes which are structurally equivalent must also be regularly equivalent, but not vice versa. The seemingly circular definition of regular equivalence is most easily understood in the following way: Every class of regularly equivalent nodes is represented by a single node in an “image graph”. The nodes in the image graph are connected (disconnected), if connections between nodes in the respective classes exist (are absent) in the original network. In Fig. $2.1$, nodes $A$ and $B, C$ and $D$ as well as $E$ and $F$ form three classes of regular equivalence. If the network in Fig. $2.1$ represents the trade interactions on a market, we may interpret these three classes as producers, retailers and consumers, respectively. Producers sell to retailers, while retailers may sell to other retailers and consumers, which in turn only buy from retailers. The image graph (also “block” or “role model”) hence gives a bird’s-eye view of the network by concentrating on the roles, i.e., the functions, only. Note that no two nodes in the image graph may be structurally equivalent, otherwise the image graph is redundant.
统计代写|复杂网络代写complex networks代考|Block Modeling
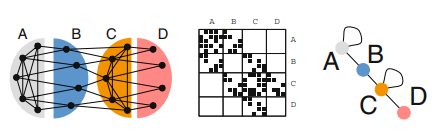
Let us consider the larger example from Fig. 2.2. The network consists of 18 nodes in 4 designed roles. Nodes of type A connect to other nodes of type $A$ and to nodes of type $B$. Those of type $B$ connect to nodes of type $A$ and $C$, Fig. 2.2. An example network and two possible block models. The nodes in this network can be grouped into four classes of regular equivalence ( $A, B, C$ and D). Ordering the rows and columns of the adjacency matrix according to the four classes of regular equivalence makes a block structure apparent (there are 16 blocks from the 4 classes), which is efficiently represented by an image graph.
acting as a kind of intermediary. Nodes of type C have connections to nodes of type $B$, others of type $C$ and of type $D$. Finally, nodes of type $D$ form a kind of periphery to nodes of type C. An ordering of rows and columns according to the types of nodes makes a block structure in the adjacency matrix apparent. Hence the name “block model”. The image graph effectively represents the 4 roles present in the original network and the 16 blocks in the adjacency matrix. Every edge present in the network is represented by an edge in the image graph and all edges absent in the image graph are also absent in the original network.
Regular equivalence, though a looser concept than structural equivalence, is still very strict as it requires the nodes to play their roles exactly, i.e., each node must have at least one of the connections required and may not have any connection forbidden by the role model. In Fig. 2.2, a link between two nodes of type A may be removed without changing the image graph, but an additional link from a node of type $A$ to a node of type $C$ would change the role model completely. Clearly, this is unsatisfactory in situations where the data are noisy or only approximate role models are desired for a very large data set.
复杂网络代写
统计代写|复杂网络代写complex networks代考|Patterns of Link Structure
上述讨论表明了研究现实世界网络中链接结构的重要性。人们可以将此问题视为一种模式检测。模式通常被视为某种规律性的表达。然而,这种规律性可能是什么,通常仍然是一个模糊的概念。将所有内容定义为非随机的规则可能是明智的。
本专着所关注的结构是复杂网络中一种特殊类型的非随机结构,与上述相关性密切相关。关于相关性的部分已经表明,如果网络中不同类型的节点是已知的,则网络的链接结构可能会显示特定的签名。然而,在大多数情况下,不同类型节点的存在只是假设,每个节点的类型是未知的。这项工作的目的是开发方法来检测网络中不同类型节点的存在并找到每个节点的推定类型。来自各个领域的许多可能的应用将再次激发这个问题。
假设我们有一个企业的通信网络。节点是雇员,链接表示它们之间的通信,例如通过电子邮件。然后,我们可能会寻找“实践社区”——彼此之间联系特别紧密的员工,即具有高度丰富的群体内交流。然后可以将这些实践社区与企业的组织结构进行比较,并可能将结果用于未来项目的团队组装。Tyler 等人已经在这个方向进行了研究。[26]。
来自生物学的新实验技术允许自动提取生物体产生的所有蛋白质。蛋白质是生物功能的核心组成部分,但通常,蛋白质不会单独发挥作用,而是相互结合形成复合物,这些复合物又能够执行特定功能,例如启动特定 DNA 片段的转录。现在可以以自动化的方式研究大量蛋白质的成对结合相互作用[27]. 这种研究的结果是一个蛋白质相互作用网络,其中的链接代表蛋白质之间的成对相互作用。蛋白质功能应该反映在这样的网络中。例如,构成复合物一部分的蛋白质现在应该可以作为此类网络中密集互连的节点组进行检测 [28]。分析蛋白质相互作用或其他生物网络的结构
因此,由自动化实验创建是规划未来实验的第一步 [29]。
科学文章的集合代表了一个高度分散的科学知识库[30,31]. 在线数据库使得以自动方式研究这些成为可能,例如以共同作者网络或引文网络的形式。在前者中,节点是研究人员,而链接代表一篇或多篇文章的共同作者。对该网络结构的分析可能会提供有关不同科学家之间合作的宝贵信息,并有助于评估资助政策或影响未来的资助决策。在后者中,网络中的节点是科学文章,链接表示对另一个的引用。分析这个网络的结构可能会深入了解特定科学领域的不同研究领域。
统计代写|复杂网络代写complex networks代考|Positions, Roles and Equivalences
通过调查来自包括生命科学、生态学、信息和社会科学以及经济学在内的广泛来源的数据,研究人员表明,网络拓扑与该网络中节点的功能之间确实存在密切关系[ 1-9]。一个中心思想是具有相似连接模式的节点将执行相似的功能。了解网络的拓扑结构将是了解单个节点功能以及最终了解任何网络动态的第一步。
和以前一样,我们可以将我们的分析建立在社会科学领域所做的工作上。在社交网络的背景下,连接模式与网络中代理的功能相关的想法被称为扮演“角色”或假设“位置”[10,11]. 在这里,我们将赞同这个想法。
网络中的节点可以根据它们所扮演的角色分为等价类。已经开发了两个基本概念来正式确定个人在社会网络中所扮演角色的分配:结构对等和常规对等。两者都如图 2.1 所示。如果两个节点具有完全相同的邻居,则称它们为结构等效的 [12]。这意味着在网络的邻接矩阵中,对应节点的行和列是完全相等的。这种等效性背后的想法是,具有完全相同交互伙伴的两个节点只能在网络中执行完全相同的功能。在图 2.1 中,只有节点一种和乙在结构上等价,而所有其他节点仅在结构上与其自身等价。
为了放宽这个非常严格的标准,引入了正则等价[13, 14]。如果两个节点以相同的方式连接到等价的其他节点,则它们通常是等价的。显然,所有结构等价的节点也必须定期等价,但反之则不然。正则等价看似循环的定义最容易理解为:每类正则等价节点都由“图像图”中的单个节点表示。如果原始网络中各个类中的节点之间存在(不存在)连接,则图像图中的节点是连接的(断开的)。在图。2.1, 节点一种和乙,C和D也和和F形成三类正则等价。如果网络如图2.1代表市场上的贸易互动,我们可以将这三类分别解释为生产者、零售商和消费者。生产者向零售商销售产品,而零售商可能向其他零售商和消费者销售产品,而消费者又只从零售商那里购买。因此,图像图(也称为“块”或“角色模型”)通过仅关注角色(即功能)来提供网络的鸟瞰图。请注意,图像图中没有两个节点在结构上可能是等效的,否则图像图是冗余的。
统计代写|复杂网络代写complex networks代考|Block Modeling
让我们考虑图 2.2 中更大的例子。该网络由 4 个设计角色的 18 个节点组成。类型 A 的节点连接到其他类型的节点一种和类型的节点乙. 那些类型乙连接到类型的节点一种和C,图 2.2。一个示例网络和两个可能的块模型。该网络中的节点可以分为四类正则等价(一种,乙,C和 D)。根据四类正则等价对邻接矩阵的行和列进行排序,使得块结构明显(4 类中有 16 个块),它可以通过图像图有效地表示。
作为一种中介。类型 C 的节点与类型的节点有连接乙, 其他类型C和类型D. 最后,节点类型D对类型 C 的节点形成一种外围。根据节点类型对行和列的排序使得邻接矩阵中的块结构变得明显。因此得名“块模型”。图像图有效地表示了原始网络中存在的 4 个角色和邻接矩阵中的 16 个块。网络中存在的每条边都由图像图中的一条边表示,并且图像图中不存在的所有边在原始网络中也不存在。
正则等价虽然是一个比结构等价更宽松的概念,但仍然非常严格,因为它要求节点准确地发挥自己的作用,即每个节点必须至少有一个所需的连接,并且不能有任何角色模型禁止的连接. 在图 2.2 中,可以在不改变图像图的情况下删除两个 A 类型节点之间的链接,但是可以从类型 A 的节点中删除一个附加链接一种到类型的节点C将彻底改变榜样。显然,这在数据嘈杂或对于非常大的数据集只需要近似角色模型的情况下是不能令人满意的。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。统计代写|python代写代考
随机过程代考
在概率论概念中,随机过程是随机变量的集合。 若一随机系统的样本点是随机函数,则称此函数为样本函数,这一随机系统全部样本函数的集合是一个随机过程。 实际应用中,样本函数的一般定义在时间域或者空间域。 随机过程的实例如股票和汇率的波动、语音信号、视频信号、体温的变化,随机运动如布朗运动、随机徘徊等等。
贝叶斯方法代考
贝叶斯统计概念及数据分析表示使用概率陈述回答有关未知参数的研究问题以及统计范式。后验分布包括关于参数的先验分布,和基于观测数据提供关于参数的信息似然模型。根据选择的先验分布和似然模型,后验分布可以解析或近似,例如,马尔科夫链蒙特卡罗 (MCMC) 方法之一。贝叶斯统计概念及数据分析使用后验分布来形成模型参数的各种摘要,包括点估计,如后验平均值、中位数、百分位数和称为可信区间的区间估计。此外,所有关于模型参数的统计检验都可以表示为基于估计后验分布的概率报表。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
statistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
机器学习代写
随着AI的大潮到来,Machine Learning逐渐成为一个新的学习热点。同时与传统CS相比,Machine Learning在其他领域也有着广泛的应用,因此这门学科成为不仅折磨CS专业同学的“小恶魔”,也是折磨生物、化学、统计等其他学科留学生的“大魔王”。学习Machine learning的一大绊脚石在于使用语言众多,跨学科范围广,所以学习起来尤其困难。但是不管你在学习Machine Learning时遇到任何难题,StudyGate专业导师团队都能为你轻松解决。
多元统计分析代考
基础数据: $N$ 个样本, $P$ 个变量数的单样本,组成的横列的数据表
变量定性: 分类和顺序;变量定量:数值
数学公式的角度分为: 因变量与自变量
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
