如果你也在 怎样代写多元统计分析Multivariate Statistical Analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
多变量统计分析被认为是评估地球化学异常与任何单独变量和变量之间相互影响的意义的有用工具。
statistics-lab™ 为您的留学生涯保驾护航 在代写多元统计分析Multivariate Statistical Analysis方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写多元统计分析Multivariate Statistical Analysis代写方面经验极为丰富,各种代写多元统计分析Multivariate Statistical Analysis相关的作业也就用不着说。
我们提供的多元统计分析Multivariate Statistical Analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
统计代写|多元统计分析代写Multivariate Statistical Analysis代考|Goal of Statistics
A main goal of statistics is to analyze data in order to obtain useful information and make important decisions. In other words, statisticians analyze data to extract useful information from the data in a sample and draw important conclusions about the population. In modern world, many important decisions are based on information from data. With the developments of modern computers and internet, massive data are available and can be easily obtained, but important information in the data may not be easily obtained without using modern statistical methods. Therefore, statistics is becoming one of the most important subjects in the 21 century, and statistical methods are among the most widely used tools in almost every area, including banks, insurance industries, economics, finance, medicine, and engineering. As a New York Times article says (August 5, 2009, For Today’s Graduate, Just One Word: Statistics): “For many different jobs in today’s world, mostly what you do is data analysis (statistics), even for jobs which seem unrelated to statistics … Many today’s decisions in industry and government are based on data analysis results. Statisticians are thus in high demand …”.
Data can be collected in many ways, such as survey, internet, company records and designed experiments. Our goal is to analyze the data to extract as much information as possible and then draw some conclusions about the whole population. For example, if a new drug is found to be effective on 20 randomly selected patients (sample) based on statistical analysis, will this drug also be effective for all patients (population)? If exam scores are found to be related to students’ IQ scores as well as students’ attitude on 50 randomly selected students (sample), is this also true for all students (population)? Such a generalization from sample to population is called statistical inference. Sometimes, however, we may just wish to obtain useful information from the sample, without necessarily making inference about the population, especially if the sample is not a random and representative sample.
In practice, data analysis often consists of two stages:
- exploratory data analysis.formal (or confirmatory) data analysis.
- In exploratory data analyses, data are simply summarized using common statistics (e.g., means, standard deviations, correlations) and are displayed using common graphical tools (e.g., histograms, boxplots, scatterplots). In this stage, we simply present and summarize the data, without trying to generalize the conclusions obtained from summary statistics and graphs to the whole population. In this stage, we do not need to make any distributional assumptions for the data, i.e., we do not need to assume that data follow certain distributions such as the normal distributions. Thus, the conclusions obtained from exploratory analysis do not depend on the validity of any assumptions. Exploratory analysis can reveal important features of the data, which may lead to preliminary conclusions. Exploratory data analysis is an important step in any data analysis and should not be skipped. However, exploratory data analysis is usually followed by a formal or confirmatory analysis, which is used to confirm the preliminary conclusions from the exploratory analysis.
- In formal (or confirmatory) data analysis, we assume models or distributions for the data or population, estimate unknown parameters in the models or distributions, and attempt to make statistical inference so that we may generalize the results based on the sample to the whole population. For example, we may assume that the population follows a normal distribution, and then we use data to estimate the parameters in the normal distribution (mean and variance). Note that the models or distributions are only assumptions, so they may not be true. In other words, the assumed models and distributions should be checked for their validity based on the data. Since the assumed models or distributions rarely hold exactly, formal analysis results should only be viewed as approximate, and it is desirable to use different statistical models or methods to further validate the results.
统计代写|多元统计分析代写Multivariate Statistical Analysis代考|Univariate Analysis
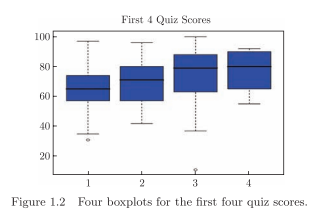
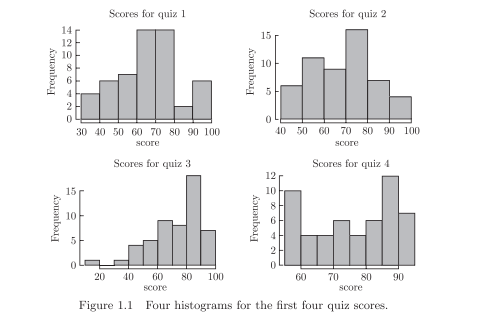
The first step in data analysis should be exploratory analysis, which summarize the data using simple statistics and display the data using graphs. Univariate continuous data are often summarized by simple statistics such as the mean and standard deviation: the mean measures the center of the data while the standard deviation measures the variation of the data. Univariate data can be displayed by graphical tools such as histogram and boxplot: a histogram show the distribution (frequencies) of the data while the boxplot shows five number summaries of the data. It is important to display data using graphs since graphs may show unusual patterns in the data and outliers. These unusual patterns and outliers may make the mean and standard deviation misleading and unreliable. A picture is worth a thousand words! Graphical tools are important components of statistical analysis.
In statistical analysis, choice of statistical methods depends on the types of data in hand. Generally, there are two types of data (or variables):
- continuous data (variables), which take continuous values.
- categorical or discrete data (variables), which take discrete values.
Examples of continuous data include weight, age, income, blood pressure, etc. Examples of categorical data include gender, location, yes/no answers, blood type, etc. Continuous data may be transformed into categorical data by grouping the data based on some threshold values, such as subjects with ages greater than 60 and subjects with ages less than or equal to 60 . Such categorizations of continuous data may simplify analysis but it may also lead to some loss of information. Note that categorical data cannot be converted to continuous data. For a categorical variable, its value may represent a category rather than a numerical value, such as gender (male/female). Statistical methods for analyzing continuous data and categorical data are quite different. In this textbook, we will mostly focus on continuous data, but we will also discuss categorical data.
Continuous data are probably most common in practice and thus will be our main focus. For univariate continuous data, the two most important features are
- the center of the data, measured by the sample mean.
- the variation of the data, measured by the sample standard deviation.
The mean and the standard deviation should always be reported in statistical analysis. They give us some idea about the average of the data and the variation in the data- the two most important features of continuous data. Note that the mean and the standard deviation can be very sensitive to outliers and the data distributions, i.e., a few outliers in the data or a severely skewed data distribution can greatly affect the values of the mean and standard deviation and thus may lead to misleading conclusions. Graphical tools such as histograms may reveal outliers and data distributions, so they should be used in data analysis.
统计代写|多元统计分析代写Multivariate Statistical Analysis代考|Multivariate Analysis
In practice, data are often collected on more than one variables, and these variables may be associated or correlated, i.e., change in one variable corresponds to changes in other variables. For example, income and education may be correlated, and gender and smoking status may be associated. When variables are associated or correlated, it is desirable to incorporate the association or correlation and analyze the data on these variables simultaneously. In other words, when several variables are associated,
it may be more desirable to use multivariate analysis than univariate analysis, since multivariate analysis uses extra information from the correlation or association. In other words, when analyzing data on one variable from a multivariate dataset, we can borrow information from data on other variables. Note that the term “correlation” is usually used for continuous data while the term “association” may be used for both continuous and discrete data. Data on two or more variables are called multivariate data, and statistical analysis of multivariate data is called multivariate analysis. In multivariate analysis, a key consideration is to incorporate the correlation or association between the variables.
Methods to measure the correlation among continuous data and methods to measure the association among discrete data are quite different. For continuous multivariate data, we usually use correlation matrices while for discrete multivariate data we usually use odds ratio or other measurements, which will be described in details in later chapters. We first focus on multivariate continuous data, where each variable is a continuous variable.
As an example for multivariate continuous data, suppose that a bank or a credit card company wish to classify all customers into two groups: individuals with good credit risks and individuals with bad credit risks. The classification can be based on customers’ education $\left(x_{1}\right)$, income $\left(x_{2}\right)$, age $\left(x_{3}\right)$, and past credit history $\left(x_{4}\right)$. It would be easy to do the classification if we just consider one variable, say income. For example, individuals with high income may be classified as good credit risk, while those with low income may be classified as bad credit risk. However, since these variables $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ may be associated, we need to consider all variables simultaneously. The classification based on all variables can be challenging. For example, an individual with high income may have low education and young age. Therefore, special multivariate analysis methods are required to do the classification.
多元统计分析代考
统计代写|多元统计分析代写Multivariate Statistical Analysis代考|Goal of Statistics
统计学的一个主要目标是分析数据以获得有用的信息并做出重要的决策。换句话说,统计学家分析数据以从样本中的数据中提取有用的信息,并得出关于总体的重要结论。在现代世界中,许多重要的决策都是基于来自数据的信息。随着现代计算机和互联网的发展,海量的数据可以轻松获取和获取,但如果不使用现代统计方法,数据中的重要信息可能无法轻松获取。因此,统计学正成为 21 世纪最重要的学科之一,统计方法是几乎所有领域中使用最广泛的工具之一,包括银行、保险业、经济、金融、医学和工程。正如纽约时报的一篇文章所说(2009 年 8 月 5 日,对于今天的毕业生来说,只有一个词:统计学):“对于当今世界的许多不同工作,您所做的主要是数据分析(统计),即使是看似无关的工作到统计……当今工业和政府的许多决策都是基于数据分析结果。因此,统计学家的需求量很大……”。
可以通过多种方式收集数据,例如调查、互联网、公司记录和设计实验。我们的目标是分析数据以提取尽可能多的信息,然后得出关于整个人群的一些结论。例如,如果根据统计分析发现一种新药对 20 名随机选择的患者(样本)有效,那么该药是否也对所有患者(人群)有效?如果发现考试成绩与学生的 IQ 分数以及学生对 50 名随机选择的学生(样本)的态度有关,那么这是否也适用于所有学生(总体)?这种从样本到总体的概括称为统计推断。然而,有时我们可能只是希望从样本中获得有用的信息,而不必对总体进行推断,
在实践中,数据分析通常包括两个阶段:
- 探索性数据分析。正式(或确认)数据分析。
- 在探索性数据分析中,使用常见的统计数据(例如,平均值、标准差、相关性)简单地汇总数据,并使用常见的图形工具(例如,直方图、箱线图、散点图)显示数据。在这个阶段,我们只是简单地呈现和总结数据,而不是试图将总结统计和图表得出的结论推广到整个人群。在这个阶段,我们不需要对数据做任何分布假设,即我们不需要假设数据遵循一定的分布,例如正态分布。因此,探索性分析得出的结论不依赖于任何假设的有效性。探索性分析可以揭示数据的重要特征,从而得出初步结论。探索性数据分析是任何数据分析的重要步骤,不应跳过。但是,探索性数据分析之后通常会进行正式或确认性分析,用于确认探索性分析的初步结论。
- 在正式(或验证性)数据分析中,我们假设数据或总体的模型或分布,估计模型或分布中的未知参数,并尝试进行统计推断,以便我们可以将基于样本的结果推广到整个总体. 例如,我们可以假设总体服从正态分布,然后我们使用数据来估计正态分布中的参数(均值和方差)。请注意,模型或分布只是假设,因此它们可能不正确。换言之,应根据数据检查假设的模型和分布的有效性。由于假设的模型或分布很少完全成立,因此形式分析结果只能视为近似值,
统计代写|多元统计分析代写Multivariate Statistical Analysis代考|Univariate Analysis
数据分析的第一步应该是探索性分析,即用简单的统计数据对数据进行总结,用图表来展示数据。单变量连续数据通常用平均值和标准差等简单的统计量来概括:平均值衡量数据的中心,而标准差衡量数据的变化。单变量数据可以通过直方图和箱线图等图形工具显示:直方图显示数据的分布(频率),而箱线图显示数据的五个数字摘要。使用图表显示数据很重要,因为图表可能会显示数据和异常值中的异常模式。这些不寻常的模式和异常值可能会使均值和标准差产生误导和不可靠。一张图片胜过千言万语!
在统计分析中,统计方法的选择取决于手头数据的类型。通常,有两种类型的数据(或变量):
- 连续数据(变量),取连续值。
- 采用离散值的分类或离散数据(变量)。
连续数据的示例包括体重、年龄、收入、血压等。分类数据的示例包括性别、位置、是/否答案、血型等。连续数据可以通过基于某些方面的数据分组来转换为分类数据阈值,例如年龄大于 60 的受试者和年龄小于或等于 60 的受试者。连续数据的这种分类可以简化分析,但也可能导致一些信息丢失。请注意,分类数据不能转换为连续数据。对于一个分类变量,它的值可能代表一个类别而不是一个数值,例如性别(男/女)。分析连续数据和分类数据的统计方法是完全不同的。在这本教科书中,我们将主要关注连续数据,
连续数据可能在实践中最常见,因此将是我们的主要关注点。对于单变量连续数据,两个最重要的特征是
- 数据的中心,由样本均值测量。
- 数据的变化,由样本标准偏差测量。
应始终在统计分析中报告平均值和标准偏差。它们让我们了解数据的平均值和数据的变化——连续数据的两个最重要的特征。请注意,均值和标准差可能对异常值和数据分布非常敏感,即数据中的少数异常值或严重偏斜的数据分布会极大地影响均值和标准差的值,从而可能导致误导结论。直方图等图形工具可能会揭示异常值和数据分布,因此应在数据分析中使用它们。
统计代写|多元统计分析代写Multivariate Statistical Analysis代考|Multivariate Analysis
在实践中,数据往往是针对多个变量收集的,这些变量可能是关联的或相关的,即一个变量的变化对应于其他变量的变化。例如,收入和教育可能相关,性别和吸烟状况可能相关。当变量关联或相关时,需要合并关联或相关性并同时分析这些变量的数据。换句话说,当多个变量关联时,
使用多变量分析可能比单变量分析更可取,因为多变量分析使用来自相关性或关联性的额外信息。换句话说,当从多元数据集中分析一个变量的数据时,我们可以从其他变量的数据中借用信息。请注意,术语“相关”通常用于连续数据,而术语“关联”可用于连续数据和离散数据。关于两个或多个变量的数据称为多元数据,对多元数据进行统计分析称为多元分析。在多变量分析中,一个关键考虑因素是纳入变量之间的相关性或关联性。
衡量连续数据间相关性的方法和衡量离散数据间关联性的方法是截然不同的。对于连续的多元数据,我们通常使用相关矩阵,而对于离散的多元数据,我们通常使用优势比或其他测量方法,这将在后面的章节中详细介绍。我们首先关注多元连续数据,其中每个变量都是一个连续变量。
以多元连续数据为例,假设银行或信用卡公司希望将所有客户分为两类:信用风险良好的个人和信用风险不良的个人。分类可以根据客户的教育(X1), 收入(X2), 年龄(X3),以及过去的信用记录(X4). 如果我们只考虑一个变量,比如收入,就很容易进行分类。例如,高收入的个人可能被归类为良好的信用风险,而低收入的个人可能被归类为不良信用风险。然而,由于这些变量(X1,X2,X3,X4)可能是相关的,我们需要同时考虑所有变量。基于所有变量的分类可能具有挑战性。例如,高收入的个人可能受教育程度低且年龄较小。因此,需要特殊的多元分析方法来进行分类。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
