如果你也在 怎样代写蒙特卡洛方法Monte Carlo method这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
蒙特卡洛方法,或称蒙特卡洛实验,是一类广泛的计算算法,依靠重复随机抽样来获得数值结果。其基本概念是利用随机性来解决原则上可能是确定性的问题。
statistics-lab™ 为您的留学生涯保驾护航 在代写蒙特卡洛方法Monte Carlo method方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写蒙特卡洛方法Monte Carlo method代写方面经验极为丰富,各种代写蒙特卡洛方法Monte Carlo method相关的作业也就用不着说。
我们提供的蒙特卡洛方法Monte Carlo method及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
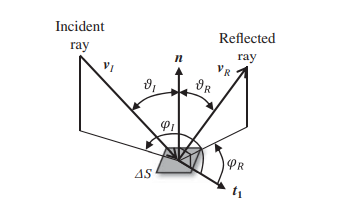
统计代写|蒙特卡洛方法代写Monte Carlo method代考|Binning of Rays on a Surface Element; Illustrative Example
Meshing and indexing are treated in Section 1.6. A closely related idea is binning, in which indexing allows us to keep track of the spatial distribution of absorbed energy bundles. In the case of the instrument in Figure 3.2, it might be desirable to know how the power incident to the entrance aperture is distributed across the detector face. In this situation, after executing Step 11, control is transferred to a binning step not shown in Figure 3.1. The detector surface, subdivided into a number of bins, is illustrated in Figure 3.5. In a given application the actual number of bins and their spatial distribution would be dictated by the shape of the surface and the desired spatial resolution.
No attempt has been made in creating Figure $3.5$ to suggest a particular scheme for determining the spacing between consecutive radial rings. However, two schemes come to mind: (i) either the ring boundaries could be equally spaced or (ii) they could be spaced to achieve equal-area rings. The former scheme is, of course, easy to achieve but is probably
not as useful as the latter. A plot of power absorbed as a function of radial position would be easier to interpret if the rings were divided into equal areas. This may be achieved using the formula
$$
r_{m}=(d / 2) \sqrt{m / M}
$$
where $d$ is the diameter of the detector, $M$ is the total number of radial bands to be created, and $r_{m}$ is the radial position of the outer radius of the $m$ th band. It is both natural and convenient to base the circumferential divisions on equal angles,
$$
\varphi_{n}=2 \pi n / N,
$$
where $N$ is the total number of angular sectors, $n$ is the $n$th such sector, and $\varphi_{n}$ is the angle corresponding to the upper angular limit of the sector.
We arrive at the binning step with knowledge of $x_{1}, y_{1}, z_{1}$, and $P_{1}$, where $P_{1}$ is the power carried by the current ray. The Matlab function for determining the values of $m$ and $n$ and updating the power accumulated in bin $(m, n)$ appears in Figure 3.6. The “floor” operator on lines 8 and 12 of Figure $3.6$ returns the least integer in the argument.
统计代写|蒙特卡洛方法代写Monte Carlo method代考|Thermal and Optical Analysis
Figure $3.7$ is a detailed data sheet for the radiometric instrument concept illustrated in Figure 3.2. Our task is to provide a preliminary evaluation of its optical and thermal performance. The approach is to model the
optical behavior of the instrument under the assumption of specularly reflecting mirrors and diffuse-specular non-mirror surfaces in the visible wavelength range $(0.4-0.7 \mu \mathrm{m})$, and to model the thermal behavior of the instrument in the infrared. Optical characterization will require assessment of baffle and telescope performance, while thermal characterization will require estimation of the distribution factor matrix. The listing for the Matlab code developed to accomplish this task is available at the companion website listed on p. xix. Study of the code listing reveals that the component geometries and dimensions have been entered “by hand.” However, it is possible to import system geometries directly into Matlab from the CAD environment where they were created.
The first step is to determine the distance from the entrance aperture to the focal plane. This task is accomplished by performing a numerical experiment in which an on-axis collimated beam consisting of 100000 rays is introduced through the instrument aperture. The detector is then displaced back and forth along the optical axis until the waist diameter of the twice-reflected beam is minimized. The result of this process, obtained by iteration, is shown in Figure 3.8, in which the rays have converged to a circle of minimum diameter at $z=58.5823 \mathrm{~mm}$. The notation “TBD” in Figure $3.7$ can now be replaced with this value, and the preliminary design of the instrument is complete.
In Figures $3.9$ and 3.10, the intersections of rays with the primary and secondary mirrors are shown as individual dots. These and similar plots for the other surfaces of the instrument are invaluable for confirming the basic design assumptions, such as symmetry in this example.
统计代写|蒙特卡洛方法代写Monte Carlo method代考|Use of Radiation Distribution Factors for the Case of Specified Surface Temperatures
Consider the special case where all of the surface elements making up the generic enclosure shown schematically in Figure $3.17$ have specified temperatures, and where all of the surface net heat fluxes are unknown. Note that the view of some surface elements may be either partially or fully blocked when viewed from other surface elements. This does not present a problem in the following analysis because partial or full blockage of direct radiation has already been accounted for in the definition and estimation of the distribution factors, as has the effect of surface curvature.
Consistent with the definition of the diffuse-specular graybody radiation distribution factor, we can express the radiation heat flux $\left(\mathrm{W} \mathrm{m}^{-2}\right.$ )
absorbed by surface element $i$ due to emission from all of the surface elements making up the enclosure
$$
q_{i, a}=\frac{Q_{i, a}}{A_{i}}=\frac{1}{A_{i}} \sum_{j=1}^{n} \varepsilon_{j} A_{j} \sigma T_{j}^{4} D_{j i}, \quad 1 \leq i \leq n,
$$
which, with the introduction of reciprocity, Eq. (3.5), becomes
$$
q_{i, a}=\varepsilon_{i} \sum_{j=1}^{n} \sigma T_{j}^{4} D_{i j} . \quad 1 \leq i \leq n .
$$
The radiation heat flux emitted from surface element $i$ is
$$
q_{i, e}=\frac{Q_{i, e}}{A_{i}}=\frac{\varepsilon_{i} A_{i} \sigma T_{i}^{4}}{A_{i}}=\varepsilon_{i} \sigma T_{i}^{4}, \quad 1 \leq i \leq n
$$
Then the net heat flux from surface element $i$ is
$$
q_{i}=q_{i, e}-q_{i, a}=\varepsilon_{i} \sigma T_{i}^{4}-\varepsilon_{i} \sum_{j=1}^{n} \sigma T_{j}^{4} D_{i j}, \quad 1 \leq i \leq n
$$
or, with the introduction of the Kronecker delta
$$
\delta_{i j} \equiv \begin{cases}1, & i=j \ 0, & i \neq j\end{cases}
$$
Eq. (3.33) can be written
$$
q_{i}=\varepsilon_{i} \sum_{j=1}^{n} \sigma T_{j}^{4}\left(\delta_{i j}-D_{i j}\right) \quad 1 \leq i \leq n
$$
蒙特卡洛方法代考
统计代写|蒙特卡洛方法代写Monte Carlo method代考|Binning of Rays on a Surface Element; Illustrative Example
网格化和索引在 1.6 节中讨论。一个密切相关的想法是分箱,其中索引允许我们跟踪吸收的能量束的空间分布。对于图 3.2 中的仪器,可能需要知道入射到入口孔径的功率如何在探测器表面上分布。在这种情况下,执行步骤 11 后,控制转移到图 3.1 中未显示的分箱步骤。检测器表面被细分为多个 bin,如图 3.5 所示。在给定的应用中,实际的 bin 数量及其空间分布将由表面的形状和所需的空间分辨率决定。
没有尝试创建Figure3.5建议确定连续径向环之间间距的特定方案。然而,我想到了两种方案:(i)环边界可以等间距或(ii)它们可以隔开以实现等面积的环。前一种方案当然很容易实现,但可能
不如后者有用。如果将环分成相等的区域,则作为径向位置函数的吸收功率图将更容易解释。这可以使用公式来实现
r米=(d/2)米/米
在哪里d是探测器的直径,米是要创建的径向带的总数,并且r米是外半径的径向位置米乐队。以等角为基础的圆周划分既自然又方便,
披n=2圆周率n/ñ,
在哪里ñ是角扇区的总数,n是个n此类部门,以及披n是对应于扇区角上限的角度。
我们到达装箱步骤时知道X1,是1,和1, 和磷1, 在哪里磷1是当前射线携带的能量。用于确定值的 Matlab 函数米和n并更新 bin 中累积的功率(米,n)如图 3.6 所示。图的第 8 行和第 12 行的“floor”运算符3.6返回参数中的最小整数。
统计代写|蒙特卡洛方法代写Monte Carlo method代考|Thermal and Optical Analysis
数字3.7是图 3.2 中所示的辐射测量仪器概念的详细数据表。我们的任务是对其光学和热性能进行初步评估。方法是建模
假设镜面反射镜和漫反射非镜面在可见波长范围内的仪器光学行为(0.4−0.7μ米),并模拟仪器在红外线中的热行为。光学特性需要评估挡板和望远镜的性能,而热特性需要估计分布因子矩阵。为完成此任务而开发的 Matlab 代码清单可在第 4 页列出的配套网站上找到。十九。对代码清单的研究表明,组件的几何形状和尺寸是“手工”输入的。但是,可以将系统几何图形从创建它们的 CAD 环境直接导入 Matlab。
第一步是确定从入口孔径到焦平面的距离。这项任务是通过进行数值实验来完成的,在该实验中,由 100000 条光线组成的轴上准直光束通过仪器孔径引入。然后检测器沿光轴来回移动,直到两次反射光束的腰部直径最小。这个过程通过迭代得到的结果如图 3.8 所示,其中光线在和=58.5823 米米. 图中的符号“TBD”3.7现在可以用这个值代替,仪器的初步设计就完成了。
在数字3.9在图 3.10 和 3.10 中,光线与主镜和次镜的交点显示为单独的点。仪器其他表面的这些和类似图对于确认基本设计假设(例如本例中的对称性)非常宝贵。
统计代写|蒙特卡洛方法代写Monte Carlo method代考|Use of Radiation Distribution Factors for the Case of Specified Surface Temperatures
考虑一种特殊情况,其中所有表面元素构成图 1 中示意性地显示的通用外壳。3.17具有指定的温度,并且所有表面净热通量都是未知的。请注意,当从其他表面元素查看时,某些表面元素的视图可能会部分或完全被遮挡。这在下面的分析中不会出现问题,因为在分布因子的定义和估计中已经考虑了直接辐射的部分或完全阻挡,表面曲率的影响也是如此。
与漫反射灰体辐射分布因子的定义一致,可以表示辐射热通量(在米−2 )
被表面元素吸收一世由于构成外壳的所有表面元素的发射
q一世,一个=问一世,一个一个一世=1一个一世∑j=1nej一个jσ吨j4Dj一世,1≤一世≤n,
其中,随着互惠的引入,方程式。(3.5),变为
q一世,一个=e一世∑j=1nσ吨j4D一世j.1≤一世≤n.
面元发出的辐射热通量一世是
q一世,和=问一世,和一个一世=e一世一个一世σ吨一世4一个一世=e一世σ吨一世4,1≤一世≤n
然后是来自表面元素的净热通量一世是
q一世=q一世,和−q一世,一个=e一世σ吨一世4−e一世∑j=1nσ吨j4D一世j,1≤一世≤n
或者,随着克罗内克三角洲的引入
d一世j≡{1,一世=j 0,一世≠j
方程。(3.33) 可以写成
q一世=e一世∑j=1nσ吨j4(d一世j−D一世j)1≤一世≤n
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
