如果你也在 怎样代写金融中的随机方法Stochastic Methods in Finance这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
随机建模是金融模型的一种形式,用于帮助做出投资决策。这种类型的模型使用随机变量预测不同条件下各种结果的概率。随着现代经济学、金融学实证研究的发展,金融中的随机方法Stochastic Methods in Finance作为一种数学工具具有越来越重要的应用价值。
statistics-lab™ 为您的留学生涯保驾护航 在代写金融中的随机方法Stochastic Methods in Finance方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写金融中的随机方法Stochastic Methods in Finance方面经验极为丰富,各种代写金融中的随机方法Stochastic Methods in Finance相关的作业也就用不着说。
我们提供的金融中的随机方法Stochastic Methods in Finance及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等楖率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
统计代写|金融中的随机方法作业代写Stochastic Methods in Finance代考|Casualty Insurance
Increasing competition in the insurance sector in developed countries, and more recently record property and casualty $(\mathrm{P \& C}$ ) insurance claims reported by global players (CEA, 2010; Europe Economics, 2010), has gencrated remarkable
pressures on the financial stability of $\mathrm{P} \& \mathrm{C}$ divisions within insurance firms, leading to increased technical reserves and requiring a higher capital base (European Parliament, 2009). At the same time we have witnessed a remarkable expansion of investment management divisions, reinforcing the role of insurers as institutional investors competing in fixed income and equity markets with other players such as pension and mutual funds. Increasing market volatility in the last few years has, as a result, affected large insurers’ market risk exposure. Regulatory bodies, through the Solvency II regulation (European Parliament, 2009; ISVAP, 2010), have supported risk-based capital allocation measures for insurance firms as a whole. As a response large insurance companies have pursued restructuring aimed from an operational perspective at integrating the historical insurance business with the investment management business. Such an integration is also motivated by the perceived role of the $\mathrm{P} \& \mathrm{C}$ division as a liquidity buffer for the cash deficits generated by fixed income portfolios typically held by risk-averse investment divisions. A trade-off between safe liquidity conditions, key to shareholders’ short-mediumterm returns, and long-term business sustainability has emerged and lead to strategies based on long-term horizons. This motivates the adoption of a multistage stochastic programming (MSP) problem formulation (Birge and Louveaux, 1997; Cariño et al., 1994; Consigli and Dempster, 1998; Mulvey and Erkan, 2005; Zenios and Ziemba, 2007a) able to capture both short- and long-term goals. Contrary to current standards in insurance-based investment divisions which largely rely on one-period static approaches (de Lange et al., 2003; Mulvey and Erkan, 2003; Zenios and Ziemba, 2007b), the adoption of dynamic approaches allows both the extension of the decision horizon and a more accurate short-term modelling of $P \& C$ variables.
In this chapter we present an asset-liability management (ALM) problem integrating the definition of an optimal asset allocation policy over a 10-year planning horizon with the inclusion of liability constraints generated by an ongoing P\&C business (de Lange et al., 2003; Dempster et al., 2003; Mulvey and Erkan, 2005; Mulvey et al., 2007). Relying on a simplified P\&C income statement we clarify the interaction between the investment and the classical insurance business and introduce an objective function capturing short-, medium-, and long-term goals within a multistage model. The planning horizon is divided in six time periods: four quarters in the first year and then 2 and 7 years to reach the 10 -year horizon. Over this period alternative insurance and financial scenarios will affect the insurance management optimal forward policy. We show that integrated management of the insurance liability and asset portfolios is required to protect firm solvency in the presence of unexpectedly increased P\&C claims. A relatively simple multivariate Gaussian return model is adopted to generate return scenarios (Dupačová et al., 2001) for a realistic investment universe including fixed income, equity, and real estate investment opportunities.
统计代写|金融中的随机方法作业代写Stochastic Methods in Finance代考|P&C Income Generation and Asset Allocation
We consider an insurance company holding a property and casualty liability portfolio with annual issuance of insurance contracts and a diversified asset portfolio spanning fixed income, real estate, and equity markets. The insurance management sets a target for the end-of-the-year operating profit on an annual basis and seeks an optimal trade-off between this short-term goal, medium-term industrial plan targets, and a (10-year) long-term sustainability goal. The company’s financial soundness will depend on the solidity of both the $\mathrm{P} \& \mathrm{C}$ business division, hereafter also referred to as the technical division, and the imvestment division. In a simplified framework, with stable insurance provisions and reserves, we assume that technical profitability primarily depends on collected annual premiums, operating and human resource costs, and, crucially, recorded insurance claims. We assume throughout that the company will fix insurance premiums so as to maintain its market position within a highly competitive market and that the operational efficiency with minimal operating, staff and administrative costs is maintained over time exogenously to the optimal financial management problem. In this setting alternative insurance claim scenarios are likely from 1 year to the next to heavily affect the company technical profitability. Increasing technical provisions may, on the other hand, weaken the capital base. This is indeed the risk faced currently by several global players in the insurance sector (Europe Economics, 2010), with record claims in the automotive and increasingly the real estate sector, and regarding catastrophic events (CAT risk events). Under such conditions the management will search for an asset portfolio strategy able to preserve the firm’s liquidity in the short term and its overall sustainability in the long term. Only the first goal ean be aecommodated within
a static 1-year decision problem. The investment profit depends on realized price gains from trading, dividends, and interest cash flows generated by the asset portfolio; see Table 5.1. Risky investment strategies may very well generate sufficient liquidity and financial profit over I year but then lead to heavy long-term losses, jeopardizing the company’s market position and solvency. Revenues and costs, as shown in Table $5.1$, will affect annually the firm’s profitability and are considered in the ALM model formulation.
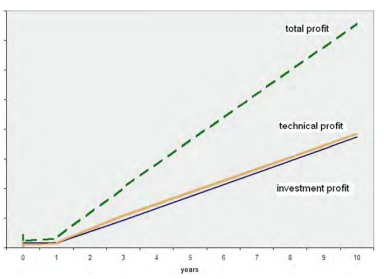
The P\&C annual operating profit does not consider the portfolio’s gain and losses, which, if unrealized, reflect the asset portfolio’s revaluation over time (and can translate into current realized gains or losses if required). If actually realized portfolio profits and losses are nevertheless considered outside the core insurance activity. Net of future liabilities, the maximization of the investment portfolio expected value, can thus be considered a medium-term goal to be pursued by the management. Realized investment and technical profits, together with unrealized gains, will eventually jointly determine the business long-term sustainability reflected in the 10-year target. We assume a 10-year decision horizon with the first year divided into four quarters, a subsequent 2 -year stage and a final 7 -year stage as shown in Fig. 5.1.
统计代写|金融中的随机方法作业代写Stochastic Methods in Finance代考|Asset–Liability Management for P&C Companies
A generic P\&C ALM problem relies on the specification by the insurance firm’s actuarial division of the reserves and expected cash flows from premiums and insurance claims. In a multistage approach such inputs provide a first-year average scenario to depart from in order to assess, assuming ongoing business, the effects of these departures on longer term technical scenarios and to find an optimal asset management strategy under exogenous liquidity constraints. This set of scenario-dependent variables reflects the uncertainty faced by management in a dynamic framework. As shown in Fig. $5.1$ the initial model decision at time $t=0$ is the only one taken under full uncertainty, while subsequent decisions will all depend on previous decisions and future residual uncertainty. Such uncertainty is modelled through a scenario tree (Consigli et al., 2010; Dupačová et al., 2001; Kouwenberg, 2001; Pflug and Römisch, 2007) such as the one shown schematically in Fig. 5.3: every path, from the root node to a leaf node at the 10 -year horizon represents a scenario.
The stochastic programming formulation relies on the specification of the underlying random factors as tree processes endowed with a given branching structure. In the formulation of the ALM problem we denote by $R(t, s)$ the insurance premiums collected in stage $t$ under scenario $s$. Premiums represent the fundamental cash flows generated every year by the technical business. For given P\&C contract renewals, the insurance actuarial division will periodically revise its estimate on forthcoming claims $L(t, s)$ and required statutory and discretional reserves $\Lambda(t, s)$. These quantities for given human resources and administrative costs $C(t, s)$ will determine the behaviour of the company’s combined ratio: this is the ratio of all insurance
claims and technical costs to the earned premiums. A bad liability scenario will thus be associated with increasing insurance claims at a time of reducing premium renewals and operational inefficiency. Consequently the ex post combined ratio will increase and may go over the $100 \%$ threshold. The firm’s investment profit, instead, is generated by realized capital gains $G(t, s)$ in stage $t$, scenario $s$; the interest margin, defined as the difference between positive and negative interest cash flows, $M(t, s)=I^{+}(t, s)-I^{-}(t, s)$; and by dividends $D(t, s)$ and other financial revenues $Y(t, s)$.
The annual income $\Pi(t, s)$ is determined by the sum of technical and investment profit. The net income, here assumed entirely distributed, is derived by subtracting the corporate tax $T$ from the profit $D^{-}(t, s)=\Pi(t, s)(1-T)$.
金融中的随机方法代写
统计代写|金融中的随机方法作业代写Stochastic Methods in Finance代考|Casualty Insurance
发达国家保险业的竞争日益激烈,最近的财产和伤亡人数创纪录(磷&C) 全球参与者报告的保险索赔(CEA,2010 年;欧洲经济,2010 年),已经产生了显着的
金融稳定的压力磷&C保险公司内部的分工,导致技术储备增加并需要更高的资本基础(欧洲议会,2009 年)。与此同时,我们见证了投资管理部门的显着扩张,加强了保险公司作为机构投资者的作用,在固定收益和股票市场上与养老金和共同基金等其他参与者竞争。因此,过去几年市场波动的加剧影响了大型保险公司的市场风险敞口。监管机构通过偿付能力 II 监管(欧洲议会,2009 年;ISVAP,2010 年)支持整个保险公司基于风险的资本分配措施。作为回应,大型保险公司从运营角度寻求重组,旨在整合历史保险业务与投资管理业务。这种整合也是由感知到的角色所推动的。P&C部门作为流动性缓冲,以应对通常由规避风险的投资部门持有的固定收益投资组合产生的现金赤字。安全流动性条件、股东中短期回报的关键和长期业务可持续性之间的权衡已经出现,并导致基于长期视野的战略。这促使采用多阶段随机规划 (MSP) 问题公式(Birge 和 Louveaux,1997 年;Cariño 等人,1994 年;Consigli 和 Dempster,1998 年;Mulvey 和 Erkan,2005 年;Zenios 和 Ziemba,2007a)能够同时捕获两者短期和长期目标。与主要依赖单期静态方法的保险投资部门的现行标准相反(de Lange 等人,2003;Mulvey 和 Erkan,2003;Zenios 和 Ziemba,2007b),磷&C变量。
在本章中,我们提出了一个资产负债管理 (ALM) 问题,该问题将 10 年规划范围内的最优资产配置政策的定义与正在进行的 P&C 业务产生的负债约束相结合(de Lange et al. , 2003 年;Dempster 等人,2003 年;Mulvey 和 Erkan,2005 年;Mulvey 等人,2007 年)。依靠简化的 P&C 损益表,我们阐明了投资与经典保险业务之间的相互作用,并在多阶段模型中引入了捕获短期、中期和长期目标的目标函数。规划期限分为六个时间段:第一年的四个季度,然后是 2 年和 7 年,直至 10 年。在此期间,替代保险和金融情景将影响保险管理的最佳远期保单。我们表明,保险负债和资产组合的综合管理是在意外增加的 P&C 索赔的情况下保护公司偿付能力所必需的。采用相对简单的多元高斯回报模型来为包括固定收益、股权和房地产投资机会在内的现实投资领域生成回报情景 (Dupačová et al., 2001)。
统计代写|金融中的随机方法作业代写Stochastic Methods in Finance代考|P&C Income Generation and Asset Allocation
我们考虑一家保险公司,其持有财产和意外伤害责任投资组合,每年发行保险合同,资产组合多元化,涵盖固定收益、房地产和股票市场。保险管理层每年设定年终营业利润目标,并在此短期目标、中期产业计划目标和(10 年)长期目标之间寻求最佳平衡。长期可持续发展目标。公司的财务稳健性将取决于双方的稳健性磷&C业务部,以下也称技术部、投资部。在一个简化的框架中,在保险准备金和准备金稳定的情况下,我们假设技术盈利能力主要取决于收取的年度保费、运营和人力资源成本,以及至关重要的保险理赔记录。我们始终假设公司将固定保险费以在竞争激烈的市场中保持其市场地位,并且随着时间的推移,以最小的运营、员工和行政成本维持运营效率,以优化财务管理问题。在这种情况下,替代的保险索赔方案可能会从一年到下一年严重影响公司的技术盈利能力。另一方面,增加技术规定可能会 削弱资本基础。这确实是保险行业的几家全球参与者目前面临的风险(Europe Economics,2010),汽车和越来越多的房地产行业的索赔创纪录,以及灾难性事件(CAT 风险事件)。在这种情况下,管理层将寻求一种能够在短期内保持公司流动性并在长期内保持整体可持续性的资产组合策略。只有第一个目标可以容纳在 在这种情况下,管理层将寻求一种能够在短期内保持公司流动性并在长期内保持整体可持续性的资产组合策略。只有第一个目标可以容纳在 在这种情况下,管理层将寻求一种能够在短期内保持公司流动性并在长期内保持整体可持续性的资产组合策略。只有第一个目标可以容纳在
一个静态的 1 年决策问题。投资利润取决于资产组合产生的交易、股息和利息现金流的实现价格收益;见表 5.1。高风险的投资策略很可能在一年内产生足够的流动性和财务利润,但随后会导致严重的长期亏损,危及公司的市场地位和偿付能力。收入和成本,如表所示5.1,每年都会影响公司的盈利能力,并在 ALM 模型制定中予以考虑。
P\&C 年度营业利润不考虑投资组合的损益,如果未实现,则反映资产组合随时间的重估(如果需要,可以转化为当前已实现的损益)。如果实际实现的投资组合利润和损失仍然被视为核心保险活动之外。因此,扣除未来负债后,投资组合预期价值的最大化可以被视为管理层追求的中期目标。已实现的投资和技术利润,以及未实现的收益,最终将共同决定10年目标所体现的业务长期可持续性。我们假设一个 10 年的决策期限,第一年分为四个季度,随后是 2 年阶段和最后 7 年阶段,如图 5.1 所示。
统计代写|金融中的随机方法作业代写Stochastic Methods in Finance代考|Asset–Liability Management for P&C Companies
一般的 P\&C ALM 问题依赖于保险公司精算部门对准备金和保费和保险索赔的预期现金流量的规范。在多阶段方法中,这些输入提供了一个第一年的平均情景,以便在假设正在进行的业务的情况下评估这些偏离对长期技术情景的影响,并在外生流动性约束下找到最佳资产管理策略。这组情景相关变量反映了动态框架中管理层面临的不确定性。如图所示。5.1时间的初始模型决策吨=0是唯一在完全不确定的情况下做出的决定,而随后的决定都将取决于先前的决定和未来的剩余不确定性。这种不确定性通过情景树(Consigli et al., 2010; Dupačová et al., 2001; Kouwenberg, 2001; Pflug and Römisch, 2007)建模,如图 5.3 所示:每条路径,从根节点到 10 年范围内的叶节点代表一个场景。
随机规划公式依赖于将潜在随机因素指定为具有给定分支结构的树过程。在 ALM 问题的表述中,我们表示为R(吨,s)分期收取的保费吨情景下s. 保费代表了技术业务每年产生的基本现金流。对于给定的财产险合同续签,保险精算部门将定期修改其对即将发生的索赔的估计大号(吨,s)以及所需的法定和酌情准备金Λ(吨,s). 给定人力资源和管理成本的这些数量C(吨,s)将决定公司行为的综合比率:这是所有保险的比率
已赚取保费的索赔和技术成本。因此,在保费续约减少和运营效率低下的情况下,不良责任情况将与增加的保险索赔相关联。因此,事后综合比率将增加,并可能超过100%临界点。相反,公司的投资利润是由已实现的资本收益产生的G(吨,s)在阶段吨, 设想s; 息差,定义为正负利息现金流之间的差额,米(吨,s)=一世+(吨,s)−一世−(吨,s); 并通过股息D(吨,s)和其他财政收入是(吨,s).
年收入圆周率(吨,s)由技术利润和投资利润之和决定。此处假设完全分配的净收入是通过减去公司税得出的吨从利润D−(吨,s)=圆周率(吨,s)(1−吨).
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。统计代写|python代写代考
随机过程代考
在概率论概念中,随机过程是随机变量的集合。 若一随机系统的样本点是随机函数,则称此函数为样本函数,这一随机系统全部样本函数的集合是一个随机过程。 实际应用中,样本函数的一般定义在时间域或者空间域。 随机过程的实例如股票和汇率的波动、语音信号、视频信号、体温的变化,随机运动如布朗运动、随机徘徊等等。
贝叶斯方法代考
贝叶斯统计概念及数据分析表示使用概率陈述回答有关未知参数的研究问题以及统计范式。后验分布包括关于参数的先验分布,和基于观测数据提供关于参数的信息似然模型。根据选择的先验分布和似然模型,后验分布可以解析或近似,例如,马尔科夫链蒙特卡罗 (MCMC) 方法之一。贝叶斯统计概念及数据分析使用后验分布来形成模型参数的各种摘要,包括点估计,如后验平均值、中位数、百分位数和称为可信区间的区间估计。此外,所有关于模型参数的统计检验都可以表示为基于估计后验分布的概率报表。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
statistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
机器学习代写
随着AI的大潮到来,Machine Learning逐渐成为一个新的学习热点。同时与传统CS相比,Machine Learning在其他领域也有着广泛的应用,因此这门学科成为不仅折磨CS专业同学的“小恶魔”,也是折磨生物、化学、统计等其他学科留学生的“大魔王”。学习Machine learning的一大绊脚石在于使用语言众多,跨学科范围广,所以学习起来尤其困难。但是不管你在学习Machine Learning时遇到任何难题,StudyGate专业导师团队都能为你轻松解决。
多元统计分析代考
基础数据: $N$ 个样本, $P$ 个变量数的单样本,组成的横列的数据表
变量定性: 分类和顺序;变量定量:数值
数学公式的角度分为: 因变量与自变量
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
