如果你也在 怎样代写宇宙学cosmology这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
宇宙学是天文学的一个分支,涉及宇宙的起源和演变,从大爆炸到今天,再到未来。宇宙学的定义是 “对整个宇宙的大尺度特性进行科学研究”。
statistics-lab™ 为您的留学生涯保驾护航 在代写宇宙学cosmology方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写宇宙学cosmology代写方面经验极为丰富,各种代写宇宙学cosmology相关的作业也就用不着说。
我们提供的宇宙学cosmology及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
物理代写|宇宙学代写cosmology代考|The concordance model of cosmology
Einstein’s discovery of general relativity in the previous century enabled us, for the first time in history, to come up with a compelling, testable theory of the universe. The realization that the universe is expanding and was once much hotter and denser allows us to modernize the deep age-old questions “Why are we here?” and “How did we get here?” The updated versions are now “How did the elements form?”, “Why is the universe so smooth?”, and “How did galaxies form within this smooth universe?” Remarkably, these questions and many like them have quantitative answers, answers that can be found only by combining our knowledge of fundamental physics with our understanding of the conditions in the early universe. Even more remarkably, these answers can be tested against astronomical observations. Before going into depth, we begin with a broad-brush overview of our current state of knowledge on the history of the universe in this chapter and the next.
The success of the Big Bang paradigm rests on a number of observational pillars: the Hubble diagram that measures expansion; light element abundances that are in accord with Big Bang Nucleosynthesis; temperature and polarization anisotropies in the cosmic microwave background that agree well with theory; and multiple probes of large-scale structure that also agree with the concordance model that will be described in this Chapter. This success has come at a price, however: we are now forced to introduce several ingredients that go beyond the Standard Model of particle physics (for a quick overview, see Box 1.1):
- dark matter and dark energy, which together dominate the energy budget of the universe over most of its lifetime;
- a mechanism generating the small initial perturbations out of which structure formed, the most popular explanation being inflation.
物理代写|宇宙学代写cosmology代考|A nutshell history of the universe
We have solid evidence that the universe is expanding. This means that early in its history the distance between us and distant galaxies was smaller than it is today. It is convenient to describe this effect by introducing the scale factor $a$, whose present value is set to 1 by convention. At earlier times, $a$ was smaller than it is today. We can imagine placing a grid in space as in Fig. 1.1 which expands uniformly as time evolves. Points on the grid, which correspond to observers at rest, maintain their coordinates, so the comoving distance between two points-which just measures the difference between coordinates, and can be obtained by counting grid cells as indicated in Fig. 1.1-remains constant. However, the physical distance is proportional to the scale factor, and the physical distance does evolve with time.
A directly related effect is that the physical wavelength of light emitted from a distant object is stretched out proportionally to the scale factor, so that the observed wavelength is larger than the one at which the light was emitted. It is convenient to define this stretching factor as the redshift $z$ :
$$
1+z \equiv \frac{\lambda_{\text {obs }}}{\lambda_{\text {emit }}}=\frac{a_{\text {obs }}}{a_{\text {emit }}}=\frac{1}{a_{\text {emit }}} .
$$
In addition to the scale factor and its evolution, the smooth universe is characterized by one other parameter, its geometry. There are three possibilities: Euclidean, open, or closed universes. These different possibilities are best understood by considering two freely traveling particles which start their journeys moving parallel to each other. In a Euclidean universe, often also called a “flat universe,” the particles behave as Euclid himself expected them to: their trajectories remain parallel as long as they travel freely. If the universe is closed, the initially parallel particles gradually converge, just as in the case of the 2 -sphere all lines of constant longitude meet at the North and South Poles. The analogy of a closed universe to the surface of a sphere runs even deeper: both are spaces of constant positive curvature, the former in three spatial dimensions and the latter in two. Finally, in an open universe, the initially parallel paths diverge, as would two marbles rolling off a saddle.
General relativity connects geometry to energy. Accordingly, the total energy density in the universe determines the geometry: if the density is higher than a critical value, $\rho_{\mathrm{cr}}$, which we will soon see is approximately $10^{-29} \mathrm{~g} \mathrm{~cm}^{-3}$, the universe is closed; if the density is lower, it is open. A Euclidean universe is one in which the energy density is precisely equal to critical. This seems unlikely to happen, and yet all observations indicate that the universe is Euclidean to within errors! We will later see that inflation provides a natural explanation for this fact.
物理代写|宇宙学代写cosmology代考|The Hubble diagram
If the universe is expanding as depicted in Fig. 1.1, then galaxies should be moving away from each other. We should therefore see galaxies receding from us. Hubble (1929) first found that distant galaxies are in fact all apparently receding from us, i.e. redshifted. He also noticed the trend that the velocity increases with distance. This is exactly what we expect in an expanding universe, for the physical distance between two galaxies is $d=a x$ where $x$ is the comoving distance. ${ }^{1}$ In the absence of any comoving motion, $\dot{x} \equiv d x / d t=0$ (no peculiar velocity), the relative velocity $v$ is therefore equal to
$$
v=\frac{d}{d t}(a x)=\dot{a} x=H_{0} d \quad(v \ll c),
$$
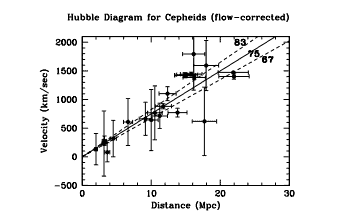
where overdots indicate derivatives with respect to time $t$. Therefore, the apparent velocity should increase linearly with distance (at least at low redshift) with a slope given by $H_{0}$, the Hubble constant. Eq. (1.8) is known as the Hubble-Lemaitre law. The value of the constant is simply determined by measuring the slope of the line in the Hubble diagram shown in Fig. 1.5.
In the next chapter, we will generalize the distance-redshift relation to larger distances, where Eq. (1.8) breaks down. Instead of recession velocities, this more rigorous derivation will be based on the stretching of the wavelength of light encoded in Eq. (1.1). For now, let us just point out that the distance-redshift relation depends on the energy content of the universe. Data from a variety of sources point to a current best-fit scenario that is Euclidean and contains about $70 \%$ of the energy in the form of a cosmological constant, or some other form of dark energy. This now forms the concordance cosmology that will be our working model throughout.
宇宙学代考
物理代写|宇宙学代写cosmology代考|The concordance model of cosmology
爱因斯坦在上个世纪发现了广义相对论,这使我们在历史上第一次提出了一个令人信服的、可检验的宇宙理论。意识到宇宙正在膨胀并且曾经变得更热、更稠密,这让我们能够将古老的古老问题现代化,“我们为什么在这里?” “我们是怎么到这里的?” 现在更新的版本是“元素是如何形成的?”、“为什么宇宙如此光滑?”和“星系是如何在这个光滑的宇宙中形成的?” 值得注意的是,这些问题以及许多类似问题都有定量的答案,只有将我们的基础物理学知识与我们对早期宇宙条件的理解结合起来才能找到答案。更值得注意的是,这些答案可以通过天文观测来检验。在深入之前,
大爆炸范式的成功依赖于许多观测支柱:测量膨胀的哈勃图;与大爆炸核合成一致的轻元素丰度;宇宙微波背景中的温度和极化各向异性与理论非常吻合;和大尺度结构的多个探针也符合本章将要描述的一致性模型。然而,这种成功是有代价的:我们现在不得不引入超出粒子物理标准模型的几种成分(快速概览,见框 1.1):
- 暗物质和暗能量,它们在宇宙生命的大部分时间里共同支配着宇宙的能量收支;
- 一种产生微小初始扰动的机制,形成结构,最流行的解释是暴胀。
物理代写|宇宙学代写cosmology代考|A nutshell history of the universe
我们有确凿的证据表明宇宙正在膨胀。这意味着在其历史早期,我们与遥远星系之间的距离比今天要小。通过引入比例因子可以方便地描述这种效果一个,其现值按惯例设置为 1。在更早的时候,一个比今天小。我们可以想象在空间中放置一个网格,如图 1.1 所示,它随着时间的推移均匀扩展。网格上的点,对应于静止的观察者,保持它们的坐标,所以两点之间的共同移动距离——它只是测量坐标之间的差异,可以通过计算网格单元来获得,如图 1.1 所示——保持不变。然而,物理距离与比例因子成正比,并且物理距离确实随着时间而变化。
一个直接相关的影响是,从远处物体发出的光的物理波长与比例因子成比例地拉伸,因此观察到的波长大于发出光的波长。将此拉伸因子定义为红移很方便和 :
1+和≡λ观测值 λ发射 =一个观测值 一个发射 =1一个发射 .
除了比例因子及其演化之外,光滑宇宙的特征还在于另一个参数,即它的几何形状。存在三种可能性:欧几里得宇宙、开放宇宙或封闭宇宙。这些不同的可能性最好通过考虑两个自由行进的粒子来理解,这两个粒子开始他们的旅程彼此平行移动。在欧几里得宇宙(通常也称为“平坦宇宙”)中,粒子的行为与欧几里得本人所期望的一样:只要它们自由行进,它们的轨迹就会保持平行。如果宇宙是封闭的,最初平行的粒子会逐渐收敛,就像在 2 球的情况下,所有恒经线在北极和南极相遇。封闭宇宙与球体表面的类比更深入:两者都是具有恒定正曲率的空间,前者在三个空间维度上,后者在两个空间维度上。最后,在一个开放的宇宙中,最初平行的路径会发散,就像两个大理石从马鞍上滚下来一样。
广义相对论将几何与能量联系起来。因此,宇宙中的总能量密度决定了几何形状:如果密度高于临界值,ρCr,我们很快就会看到大约是10−29 G C米−3,宇宙是封闭的;如果密度较低,则它是开放的。欧几里得宇宙是能量密度精确等于临界的宇宙。这似乎不太可能发生,但所有的观察都表明宇宙是欧几里得,误差范围内!稍后我们将看到通货膨胀为这一事实提供了一个自然的解释。
物理代写|宇宙学代写cosmology代考|The Hubble diagram
如果宇宙正在膨胀,如图 1.1 所示,那么星系应该彼此远离。因此,我们应该看到星系从我们身边退去。哈勃(1929)首先发现遥远的星系实际上都在明显地远离我们,即红移。他还注意到速度随距离增加的趋势。这正是我们在膨胀的宇宙中所期望的,因为两个星系之间的物理距离是d=一个X在哪里X是移动距离。1在没有任何同步运动的情况下,X˙≡dX/d吨=0(无特殊速度),相对速度在因此等于
在=dd吨(一个X)=一个˙X=H0d(在≪C),
其中过点表示关于时间的导数吨. 因此,视速度应随距离线性增加(至少在低红移处),其斜率由下式给出H0,哈勃常数。方程。(1.8) 被称为哈勃-勒梅特定律。通过测量图 1.5 所示的哈勃图中直线的斜率可以简单地确定常数的值。
在下一章中,我们将把距离-红移关系推广到更大的距离,其中方程式。(1.8) 崩溃。这种更严格的推导将基于方程式中编码的光波长的拉伸,而不是衰退速度。(1.1)。现在,让我们只指出距离-红移关系取决于宇宙的能量含量。来自各种来源的数据指向当前的最佳拟合方案,即欧几里得,包含约70%以宇宙常数或其他某种形式的暗能量形式的能量。这现在形成了和谐宇宙学,这将是我们自始至终的工作模型。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
