经济代写|博弈论代写Game Theory代考|Finitely Repeated Games
如果你也在 怎样代写博弈论Game theory 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论Game theory在20世纪50年代被许多学者广泛地发展。它在20世纪70年代被明确地应用于进化论,尽管类似的发展至少可以追溯到20世纪30年代。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
博弈论Game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
statistics-lab™ 为您的留学生涯保驾护航 在代写博弈论Game Theory方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写博弈论Game Theory代写方面经验极为丰富,各种代写博弈论Game Theory相关的作业也就用不着说。
经济代写|博弈论代写Game Theory代考|Finitely Repeated Games
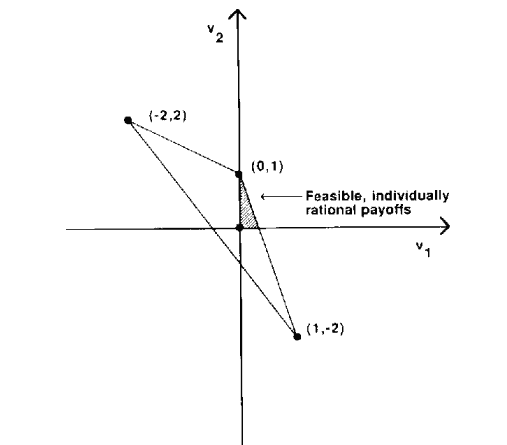
These games represent the case of a fixed known horizon $T$. The strategy spaces at each $l=0,1, \ldots, T$ are as defined above; the utilities are usually taken to be the time average of the per-period payoffs. Allowing for a discount factor $\delta$ close to 1 will not change the conclusions we present.
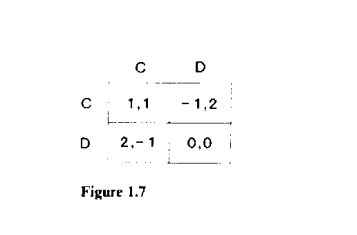
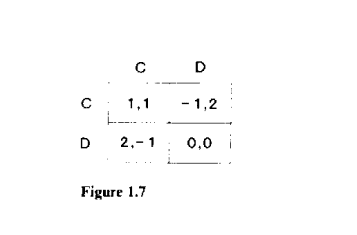
The set of equilibria of a finitely repeated game can be very different from that of the corresponding infinitely repeated game, because the scheme of self-reinforcing rewards and punishments used in the folk theorem can unravel backward from the terminal date. The classic example of this is the repeated prisoner’s dilemma. As observed in chapter 4, with a fixed finite horizon “always defect” is the only subgame-perfect-equilibrium outcome. In fact, with a bit more work one can show this is the only Nash outcome:
Fix a Nash equilibrium $\sigma^$. Both players must cheat in the last period, $T$, for any history $h^T$ that has positive probability under $\sigma^$, since doing so increases their period- $T$ payoff and since there are no future periods in which they might be punished. Next, we claim that both players must defect in period $T-1$ for any history $h^{T-1}$ with positive probability: We have already established that both players will chcat in the last period along the equilibrium path, so in particular if player $i$ conforms to the equilibrium strategy in period $T-1$ his opponent will defect in the last period, and hence player $i$ has no incentive not to defect in period $T-1$. An induction argument completes the proof. This conclusion, though not pathological, relies on the fact that the static equilibrium gives the players exactly their minmax values, as the following theorem shows.
经济代写|博弈论代写Game Theory代考|Repeated Games with Long-Run and Short-Run Players
The first variant we will consider supposes that some of the players are long-run players, as in standard repeated games, while the roles corresponding to other “players” are filled by a sequence of short-run players, each of whom plays only once.
Example 5.1
Suppose that a single long-run firm faces a sequence of short-run consumers, each of whom plays only once but is informed of all previous play when choosing his actions. Each period, the consumer moves first, and chooses whether or not to purchase a good from the firm. If the consumer does not purchase, then both players receive a payoff of 0 . If the consumer decides to purchase, then the firm must decide whether to produce high or low quality. If it produces high quality, both players have a payoff of 1 ; if it produces low quality, the firm’s payoff is 2 and the consumer’s payoff is
This game is a simplified version of those considered by Dybvig and Spatt (1980), Klein and Lefler (1981), and Shapiro (1982). ${ }^{12}$ Simon (1951)
and Kreps (1986) use a similar game to analyze the employment relationship, and to argue that one reason for the existence of “firms” is precisely to provide a long-run player who can be induced to be trustworthy by the prospect of future rewards and punishments.
The following strategies are a subgame-perfect equilibrium of this game when the firm is sufficiently patient: The firm starts out producing high yuality cvery time a consumer purchases, and continues to do so as long as it has never produced low quality in the past. If ever the firm produces low quality, it produces low quality at every subsequent opportunity. The consumers start out purchasing the good from the firm, and continue to do so so long as the firm has never produced low quality. If ever the firm produces low quality, then no consumer ever purchases again. The consumer’s strategies are optimal because each consumer cares only about that period’s payoff, and thus should buy if and only if that period’s quality is expected to be high. The firm does incur a short-run cost by producing high quality. but when the firm is patient this cost is offset by the fear that producing low quality will drive away future consumers. Note that this equilibrium suggests why consumers may prefer to deal with a firm that is expected to remain in business for a while, as opposed to a “fly-by-night” firm for whom long-run considerations are unimportant.
博弈论代考
经济代写|博弈论代写Game Theory代考|Finitely Repeated Games
这些游戏代表了一个固定已知视界$T$的情况。每个$l=0,1, \ldots, T$上的策略空间如上所述;效用通常被认为是每期收益的时间平均值。允许接近1的贴现因子$\delta$不会改变我们提出的结论。
有限重复博弈的平衡集可能与相应的无限重复博弈的平衡集非常不同,因为民间定理中使用的自我强化奖惩方案可以从结束日期向后分解。典型的例子是重复囚徒困境。正如在第4章中所观察到的,在固定的有限视界下,“总是缺陷”是唯一的子博弈-完美均衡结果。事实上,只要多做一点工作,就可以证明这是唯一的纳什结果:
修复纳什均衡$\sigma^$。两个玩家都必须在最后一个时期$T$,对于任何历史$h^T$,在$\sigma^$下有正概率,因为这样做增加了他们的时期- $T$收益,因为没有未来的时期,他们可能会受到惩罚。接下来,我们声称对于任何历史$h^{T-1}$,两个参与者都必须在时期$T-1$以正概率叛变:我们已经确定两个参与者都将在最后一个时期沿着均衡路径进行投机,所以特别是如果参与者$i$在时期$T-1$符合均衡策略,他的对手将在最后一个时期叛变,因此参与者$i$没有动机不在$T-1$时期叛变。一个归纳论证完成了这个证明。这一结论虽然不是病态的,但却是基于静态平衡能够提供给玩家最大最小值这一事实,如下面的定理所示。
经济代写|博弈论代写Game Theory代考|Repeated Games with Long-Run and Short-Run Players
我们将考虑的第一种变体假设一些玩家是长期玩家,就像在标准的重复游戏中一样,而与其他“玩家”对应的角色则由一系列短期玩家填补,每个玩家只玩一次。
例5.1
假设一个长期企业面对一系列短期消费者,每个消费者只玩一次游戏,但在选择行动时被告知之前的所有游戏。每个时期,消费者首先行动,选择是否从公司购买商品。如果消费者不购买,那么双方的收益都是0。如果消费者决定购买,那么企业必须决定生产高质量还是低质量的产品。如果产出高质量的产品,双方的收益都是1;如果生产低质量产品,公司的收益是2,消费者的收益是
这个游戏是Dybvig和Spatt (1980), Klein和Lefler(1981)以及Shapiro(1982)所考虑的游戏的简化版本。${ }^{12}$西蒙(1951)
和Kreps(1986)用一个类似的游戏来分析雇佣关系,并认为“公司”存在的一个原因正是提供一个长期的参与者,他们可以被未来的奖励和惩罚的前景诱导为值得信赖的。
当公司有足够的耐心时,以下策略是该博弈的子博弈完美均衡:每次消费者购买时,公司都会开始生产高质量的产品,并且只要它过去从未生产过低质量的产品,就会继续这样做。如果一家公司曾经生产过低质量的产品,那么它在随后的每一次机会中都会生产低质量的产品。消费者开始从公司购买商品,只要公司不生产低质量的产品,消费者就会继续购买。如果企业生产的产品质量很差,那么消费者就不会再购买。消费者的策略是最优的,因为每个消费者只关心那段时间的收益,因此当且仅当那段时间的质量预期很高时,他们才会购买。这家公司生产高质量的产品确实产生了短期成本。但是,如果企业有耐心,这种成本就会被担心生产低质量产品会赶走未来的消费者所抵消。值得注意的是,这种平衡表明了为什么消费者可能更愿意与那些有望维持一段时间的公司打交道,而不是那些对长期考虑不重要的“不可靠”的公司。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。