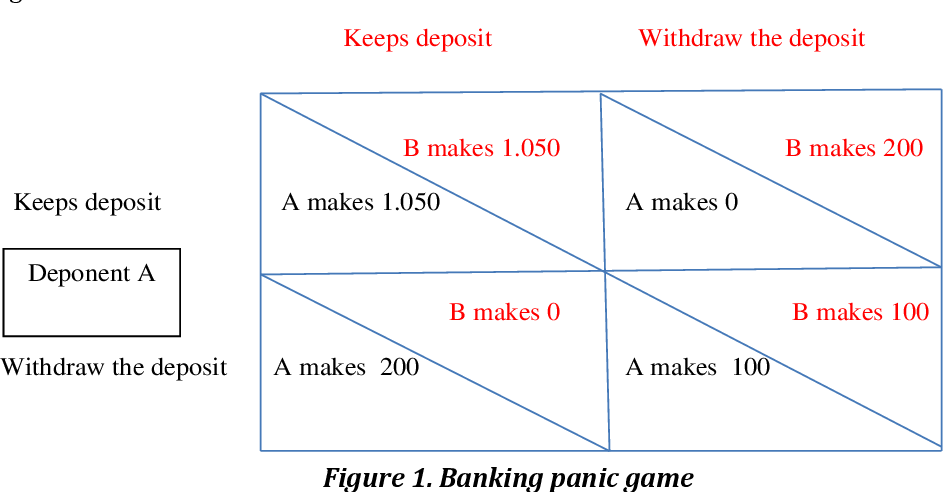
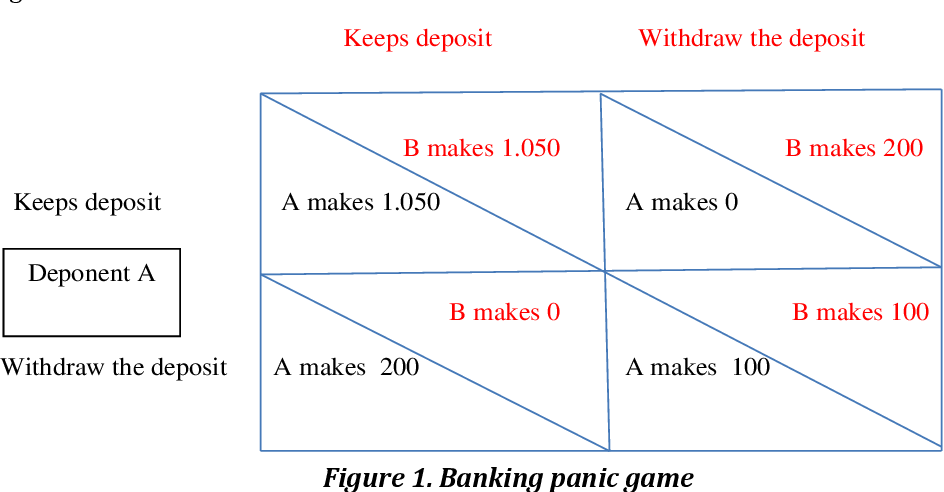
经济代写|博弈论代写Game Theory代考|CS4
如果你也在 怎样代写博弈论Game theory 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论Game theory在20世纪50年代被许多学者广泛地发展。它在20世纪70年代被明确地应用于进化论,尽管类似的发展至少可以追溯到20世纪30年代。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
博弈论Game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
statistics-lab™ 为您的留学生涯保驾护航 在代写博弈论Game Theory方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写博弈论Game Theory代写方面经验极为丰富,各种代写博弈论Game Theory相关的作业也就用不着说。
经济代写|博弈论代写Game Theory代考|Further Examples of Bayesian Equilibria
This section sketches the analyses of several Bayesian games. Although the first example is straightforward, the details of the other examples become somewhat involved, and many readers may wish to skip them. However, we refer to several of them in section 6.7.
Example 6.2: Cournot Competition with Incomplete Information Consider a duopoly playing Cournot (quantity) competition. Let firm $i$ ‘s profit be quadratic: $u_i=q_i\left(\theta_i-q_i-q_j\right)$, where $\theta_i$ is the difference between the intercept of the linear demand curve and firm i’s constant unit cost $(i-1,2)$ and where $q_i$ is the quantity chosen by firm $i\left(s_i=q_i\right)$. It is common knowledge that, for firm 1, $\theta_1=1$ (“firm 2 has complete information about firm 1,” or “firm 1 has only onc potential type”). Firm 2, however, has private information about its unit cost. Firm 1 believes that $\theta_2=\frac{3}{4}$ with probability $\frac{1}{2}$ and $\theta_2=\frac{5}{4}$ with probability $\frac{1}{2}$, and this belief is common knowledge. Thus, firm 2 has two potential types, which we will call the “low-cost type” $\left(\theta_2={ }_4^5\right)$ and the “high-cost type” $\left(\theta_2={ }_4^3\right)$. The two firms choose their outputs simultaneously.
l.ct us look for a pure-strategy equilibrium of this game. We denote firm I’s output by $q_1$, firm 2 ‘s output when $\theta_2=\frac{5}{4}$ by $q_2^{\mathrm{L}}$, and firm 2 ‘s output when $\theta_2-{ }_4^3$ by $q_2^{\mathrm{H}}$. Firm 2’s equilibrium choice $q_2\left(\theta_2\right)$ must satisfy
$$
q_2\left(\theta_2\right) \in \underset{4}{\arg \max }\left{q_2\left(\theta_2-q_1-q_2\right)\right} \Rightarrow q_2\left(\theta_2\right)=\left(\theta_2-q_1\right) / 2 .
$$
Firm I does not know which type of firm 2 it faces, so its payoff is the expected value over firm 2’s lypes:
$$
\begin{aligned}
& q_1 \subset \underset{\psi_1}{\arg \max }\left{\frac{1}{2} q_1\left(1-q_1-q_2^{\mathrm{H}}\right)+\frac{1}{2} q_1\left(1-q_1-q_2^{\mathrm{L}}\right)\right} \
& \Rightarrow q_1=-\begin{array}{r}
2-q_2^{\mathrm{H}}-q_2^{\mathrm{L}} \
4
\end{array} .
\end{aligned}
$$
经济代写|博弈论代写Game Theory代考|Interim vs. Ex Ante Dominance
If player $i$, instead of knowing the type-contingent strategies of his opponents, must try to predict them, then player $i$ must be concerned with how player $j \neq i$ thinks player $i$ would play for each possible type player $i$ might have. And player $i$ must also try to estimate player $j$ ‘s beliefs about player $i$ ‘s type, in order to predict the distribution of strategies that player $i$ expects to face.
This brings us to the question of how the players predict their opponents’ strategies, which in turn raises the following question: Should different types $\theta_1$ and $\theta_1^{\prime}$ of player 1 be viewed simply as a way of describing different information sets of a single player 1 , who makes a type-contingent decision at the ex ante stage (that is, before he learns his type)? This interpretation seems natural in the Harsanyi formulation, which introduces a move by nature that determines the “type” of a single player 1. Alternatively, should we think of $\theta_1$ and $\theta_1^{\prime}$ as denoting two different “individuals,” one of whom is selected by nature to “appear” when the game is played? In the first interpretation, the single $e x$ ante player 1 should be thought of as predicting his opponents’ play at the ex ante stage, so all types of player 1 would make the same prediction about the play of the other players. Under the second interpretation, the “different individuals” corresponding to different $\theta_1$ ‘s would each make their predictions at the “interim” stage (i.e., after learning their type), and the different types could make different predictions. (This second interpretation may become more plausible if we imagine that the “types” correspond to aspects of preferences that are genetically determined, for here the “ex ante” stage is difficult to interpret literally.)
It is inleresting to see that iterated strict dominance is at least as strong in the ex ante interpretation as in the interim interpretation and that the ex ante interpretation yields strictly stronger predictions in some games. To illustrate this, let us return to the public-good game of example 6.1. Using the interim approach to dominance, we ask which strategies are strictly dominated for player $i$ when his cost is $c_i$. Not contributing is not dominated for any positive cost level, as it is always better not to contribute if you expect that the opponent will contribute. However, if $c_i$ is greater than the private benefit of the good, which is 1 , then contributing is strictly dominated for player $i$.
博弈论代考
经济代写|博弈论代写Game Theory代考|Further Examples of Bayesian Equilibria
本节概述了几种贝叶斯博弈的分析。尽管第一个示例很简单,但其他示例的细节有些复杂,许多读者可能希望跳过它们。但是,我们将在第6.7节中提到其中的几个。
例6.2:不完全信息下的古诺竞争考虑一个双头垄断企业进行古诺(数量)竞争。坚定 $i$ 的利润是二次的: $u_i=q_i\left(\theta_i-q_i-q_j\right)$,其中 $\theta_i$ 直线需求曲线的截距和公司i不变单位成本的差是多少 $(i-1,2)$ 在哪里? $q_i$ 数量是由公司选择的吗 $i\left(s_i=q_i\right)$. 众所周知,对于公司1来说, $\theta_1=1$ (“公司2有关于公司1的完整信息”或“公司1只有一种潜在类型”)。然而,公司2拥有关于其单位成本的私人信息。公司1认为 $\theta_2=\frac{3}{4}$ 有概率地 $\frac{1}{2}$ 和 $\theta_2=\frac{5}{4}$ 有概率地 $\frac{1}{2}$,这种信念是常识。因此,公司2有两种潜在类型,我们称之为“低成本型” $\left(\theta_2={ }_4^5\right)$ 以及“高成本型” $\left(\theta_2={ }_4^3\right)$. 两家公司同时选择它们的产出。
让我们寻找这个博弈的纯策略均衡。我们用。表示公司I的输出 $q_1$时,公司2的产量 $\theta_2=\frac{5}{4}$ 通过 $q_2^{\mathrm{L}}$时,公司2的产量为 $\theta_2-{ }_4^3$ 通过 $q_2^{\mathrm{H}}$. 公司2的均衡选择 $q_2\left(\theta_2\right)$ 必须满足
$$
q_2\left(\theta_2\right) \in \underset{4}{\arg \max }\left{q_2\left(\theta_2-q_1-q_2\right)\right} \Rightarrow q_2\left(\theta_2\right)=\left(\theta_2-q_1\right) / 2 .
$$
公司I不知道它面对的是哪种类型的公司2,所以它的收益是公司2类型的期望值:
$$
\begin{aligned}
& q_1 \subset \underset{\psi_1}{\arg \max }\left{\frac{1}{2} q_1\left(1-q_1-q_2^{\mathrm{H}}\right)+\frac{1}{2} q_1\left(1-q_1-q_2^{\mathrm{L}}\right)\right} \
& \Rightarrow q_1=-\begin{array}{r}
2-q_2^{\mathrm{H}}-q_2^{\mathrm{L}} \
4
\end{array} .
\end{aligned}
$$
经济代写|博弈论代写Game Theory代考|Interim vs. Ex Ante Dominance
如果玩家$i$不知道对手的类型随机策略,而是必须尝试预测它们,那么玩家$i$就必须关注玩家$j \neq i$认为玩家$i$会如何面对玩家$i$可能拥有的每种类型。参与人$i$还必须尝试估计参与人$j$对参与人$i$类型的信念,以便预测参与人$i$期望面对的策略分布。
这就引出了玩家如何预测对手策略的问题,这反过来又提出了以下问题:玩家1的不同类型$\theta_1$和$\theta_1^{\prime}$是否应该被简单地视为描述单个玩家1的不同信息集的一种方式,而玩家1在事前阶段(即在他了解自己的类型之前)做出了类型偶然决定?这种解释在Harsanyi公式中似乎很自然,它引入了一个决定单人玩家“类型”的自然移动。或者,我们是否应该认为$\theta_1$和$\theta_1^{\prime}$表示两个不同的“个体”,其中一个在玩游戏时自然选择“出现”?在第一种解释中,单个$e x$事前玩家1应该被认为是在事前阶段预测对手的玩法,所以所有类型的玩家1都会对其他玩家的玩法做出相同的预测。在第二种解释下,不同$\theta_1$对应的“不同个体”各自在“过渡”阶段(即在学习了自己的类型之后)做出预测,不同的类型可以做出不同的预测。(如果我们想象“类型”对应于基因决定的偏好方面,第二种解释可能会变得更合理,因为这里的“事前”阶段很难从字面上解释。)
有趣的是,迭代严格支配在事前解释中至少与在临时解释中一样强大,而且事前解释在某些游戏中产生了严格更强的预测。为了说明这一点,让我们回到示例6.1中的公共利益博弈。使用优势的临时方法,我们问当玩家$i$的成本为$c_i$时,哪种策略是严格劣势的。在任何正成本水平下,不做出贡献都不是主导,因为如果你期望对手做出贡献,那么不做出贡献总是更好的选择。然而,如果$c_i$大于物品的个人利益,即1,那么对于参与者$i$来说,贡献是严格支配的。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。