如果你也在 怎样代写优化算法optimisation algorithms这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
优化算法是一个通过比较各种解决方案来反复执行的程序,直到找到一个最佳或满意的解决方案。随着计算机的出现,优化已成为计算机辅助设计活动的一部分。
statistics-lab™ 为您的留学生涯保驾护航 在代写优化算法optimisation algorithms方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写优化算法optimisation algorithms代写方面经验极为丰富,各种代写优化算法optimisation algorithms相关的作业也就用不着说。
我们提供的优化算法optimisation algorithms及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等楖率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等楖率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
数学代写|优化算法作业代写optimisation algorithms代考|Introduction – Noise
In the context of optimization, three types of noise can be distinguished. The first form is noise in the training data used as basis for learning (i). In many applications of machine learning or optimization where a model $m$ for a given system is to be learned, data samples including the input of the system and its measured response are used for training. Some typical examples of situations where training data is the basis for the objective function evaluation are
- the usage of global optimization for building classifiers (for example for predicting buying behavior using data gathered in a customer survey for training).
- the usage of simulations for determining the objective values in Genetic Programming (here, the simulated scenarios correspond to training cases), and
- the fitting of mathematical functions to $(x, y)$-data samples (with artificial neural networks or symbolic regression, for instance).
Since no measurement device is $100 \%$ accurate and there are always random errors, noise is present in such optimization problems.
Besides inexactnesses and fluctuations in the input data of the optimization process, perturbations are also likely to occur during the application of its results. This category subsumes the other two types of noise: perturbations that may arise from inaccuracies in (ii) the process of realizing the solutions
and (iii) environmentally induced perturbations during the applications of the products.
This issue can be illustrated using the process of developing the perfect tire for a car as an example. As input for the optimizer, all sorts of material coefficients and geometric constants measured from all known types of wheels and rubber could be available. Since these constants have been measured or calculated from measurements, they include a certain degree of noise and imprecision (i).
The result of the optimization process will be the best tire construction plan discovered during its course and it will likely incorporate different materials and structures. We would hope that the tires created according to the plan will not fall apart if, accidently, an extra $0.0001 \%$ of a specific rubber component is used (ii). During the optimization process, the behavior of many construction plans will be simulated in order to find out about their utility. When actually manufactured, the tires should not behave unexpectedly when used in scenarios different from those simulated (iii) and should instead be applicable in all driving scenarios likely to occur.
The effects of noise in optimization have been studied by various researchers; Miller and Goldberg $[136,137]$, Lee and Wong [125], and Gurin and Rastrigin [92] are some of them. Many global optimization algorithms and theoretical results have been proposed which can deal with noise. Some of them are, for instance, specialized
- Genetic Algorithms $[75,119,188,189,217,218]$,
- Evolution Strategies [11, 21, 96], and
- Particle Swarm Optimization [97, 161] approaches.
数学代写|优化算法作业代写optimisation algorithms代考|Need for Robustness
The goal of global optimization is to find the global optima of the objective functions. While this is fully true from a theoretical point of view, it may not suffice in practice. Optimization problems are normally used to find good parameters or designs for components or plans to be put into action by human beings or machines. As we have already pointed out, there will always be noise and perturbations in practical realizations of the results of optimization.
Definition 4 (Robustness). A system in engineering or biology is robust if it is able to function properly in the face of genetic or environmental perturbations [225].
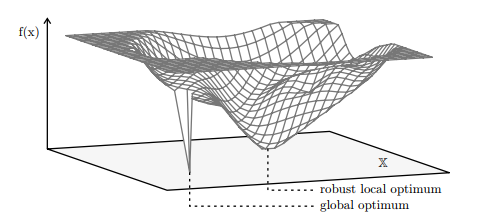
Therefore, a local optimum (or even a non-optimal element) for which slight deviations only lead to gentle performance degenerations is usually favored over a global optimum located in a highly rugged area of the fitness landscape [31]. In other words, local optima in regions of the fitness landscape with
strong causality are sometimes better than global optima with weak causality. Of course, the level of this acceptability is application-dependent. Fig. 8 illustrates the issue of local optima which are robust vs. global optima which are not. More examples from the real world are:
- When optimizing the control parameters of an airplane or a nuclear power plant, the global optimum is certainly not used if a slight perturbation can have hazardous effects on the system [218].
- Wiesmann et al [234, 235] bring up the topic of manufacturing tolerances in multilayer optical coatings. It is no use to find optimal configurations if they only perform optimal when manufactured to a precision which is either impossible or too hard to achieve on a constant basis.
- The optimization of the decision process on which roads should be precautionary salted for areas with marginal winter climate is an example of the need for dynamic robustness. The global optimum of this problem is likely to depend on the daily (or even current) weather forecast and may therefore be constantly changing. Handa et al [98] point out that it is practically infeasible to let road workers follow a constantly changing plan and circumvent this problem by incorporating multiple road temperature settings in the objective function evaluation.
- Tsutsui et al $[218,217]$ found a nice analogy in nature: The phenotypic characteristics of an individual are described by its genetic code. During the interpretation of this code, perturbations like abnormal temperature, nutritional imbalances, injuries, illnesses and so on may occur. If the phenotypic features emerging under these influences have low fitness, the organism cannot survive and procreate. Thus, even a species with good genetic material will die out if its phenotypic features become too sensitive to perturbations. Species robust against them, on the other hand, will survive and evolve.
数学代写|优化算法作业代写optimisation algorithms代考|Countermeasures
For the special case where the problem space corresponds to the real vectors $\left(\mathbb{X} \subseteq \mathbb{R}^{n}\right.$ ), several approaches for dealing with the problem of robustness have been developed. Inspired by Taguchi methods ${ }^{6}$ [209], possible disturbances are represented by a vector $\delta=\left(\delta_{1}, \delta_{2}, \ldots, \delta_{n}\right)^{T}, \delta_{i} \in \mathbb{R}$ in the method of Greiner $[87,88]$. If the distribution and influence of the $\delta_{i}$ are known, the objective function $f(\mathbf{x}): \mathbf{x} \in \mathbf{X}$ can be rewritten as $\tilde{f}(\mathbf{x}, \delta)[235] .$ In the special case where $\delta$ is normally distributed, this can be simplified to $\tilde{f}\left(\left(x_{1}+\delta_{1}, x_{2}+\delta_{2}, \ldots, x_{n}+\delta_{n}\right)^{T}\right)$. It would then make sense to sample the probability distribution of $\boldsymbol{\delta}$ a number of $t$ times and to use the mean values of $\tilde{f}(\mathbf{x}, \boldsymbol{\delta})$ for each objective function evaluation during the optimization process. In cases where the optimal value $y$ of the objective function $f$ is known, Equation 3 can be minimized. This approach is also used in the work of Wiesmann et al $[234,235]$ and basically turns the optimization algorithm into something like a maximum likelihood estimator.
$$
f^{\prime}(\mathbf{x})=\frac{1}{t} \sum_{i=1}^{t}\left(y-\bar{f}\left(\mathbf{x}, \delta_{i}\right)\right)^{2}
$$
This method corresponds to using multiple, different training scenarios during the objective function evaluation in situations where $\mathrm{X} \nsubseteq \mathbb{R}^{n}$. By adding random noise and artificial perturbations to the training cases, the chance of obtaining robust solutions which are stable when applied or realized under noisy conditions can be increased.
优化算法代考
数学代写|优化算法作业代写optimisation algorithms代考|Introduction – Noise
在优化的上下文中,可以区分三种类型的噪声。第一种形式是作为学习基础的训练数据中的噪声 (i)。在机器学习或优化的许多应用中,模型米对于要学习的给定系统,包括系统输入及其测量响应的数据样本用于训练。训练数据是目标函数评估基础的一些典型例子是
- 使用全局优化来构建分类器(例如,使用在客户调查中收集的数据来预测购买行为以进行培训)。
- 使用模拟来确定遗传编程中的目标值(这里,模拟场景对应于训练案例),以及
- 数学函数的拟合(X,是)- 数据样本(例如,使用人工神经网络或符号回归)。
由于没有测量设备100%准确且总是存在随机误差,此类优化问题中存在噪声。
除了优化过程的输入数据的不精确和波动之外,在其结果的应用过程中也可能发生扰动。此类别包含其他两种类型的噪声:可能由 (ii) 实现解决方案的过程中的不准确性引起的扰动
(iii) 产品应用过程中环境引起的扰动。
可以使用为汽车开发完美轮胎的过程来说明这个问题。作为优化器的输入,可以使用从所有已知类型的车轮和橡胶测量的各种材料系数和几何常数。由于这些常数是通过测量来测量或计算的,因此它们包含一定程度的噪声和不精确性 (i)。
优化过程的结果将是在其过程中发现的最佳轮胎构造计划,并且可能包含不同的材料和结构。我们希望根据计划制造的轮胎不会在意外发生额外的轮胎时分崩离析0.0001%(ii) 使用 100 克的特定橡胶组分。在优化过程中,将模拟许多施工计划的行为,以了解其效用。在实际制造时,轮胎在与模拟 (iii) 不同的场景中使用时不应出现意外行为,而应适用于所有可能发生的驾驶场景。
各种研究人员已经研究了噪声对优化的影响;米勒和戈德堡[136,137]、Lee 和 Wong [125],以及 Gurin 和 Rastrigin [92] 就是其中的一部分。已经提出了许多可以处理噪声的全局优化算法和理论结果。例如,其中一些是专门的
- 遗传算法[75,119,188,189,217,218],
- 进化策略 [11, 21, 96] 和
- 粒子群优化 [97, 161] 方法。
数学代写|优化算法作业代写optimisation algorithms代考|Need for Robustness
全局优化的目标是找到目标函数的全局最优值。虽然从理论的角度来看这是完全正确的,但在实践中可能还不够。优化问题通常用于为要由人类或机器付诸行动的组件或计划找到好的参数或设计。正如我们已经指出的,在优化结果的实际实现中总会存在噪声和扰动。
定义 4(稳健性)。如果工程或生物学系统能够在面对遗传或环境扰动时正常运行,那么它就是稳健的 [225]。
因此,轻微偏差只会导致轻微性能退化的局部最优(甚至非最优元素)通常优于位于健身景观高度崎岖区域的全局最优[31]。换句话说,适应度景观区域的局部最优
强因果关系有时比弱因果关系的全局最优值要好。当然,这种可接受性的程度取决于应用程序。图 8 说明了稳健的局部最优与不稳健的全局最优的问题。来自现实世界的更多例子是:
- 在优化飞机或核电站的控制参数时,如果轻微的扰动会对系统产生有害影响,则肯定不会使用全局最优值 [218]。
- Wiesmann 等人 [234, 235] 提出了多层光学涂层制造公差的主题。如果它们仅在制造到不可能或太难在恒定基础上实现的精度时才表现最佳,那么找到最佳配置是没有用的。
- 优化冬季气候边缘地区道路应预防性盐渍的决策过程是需要动态稳健性的一个例子。这个问题的全局最优可能取决于每日(甚至当前)天气预报,因此可能会不断变化。Handa 等人 [98] 指出,让道路工作人员遵循不断变化的计划并通过在目标函数评估中结合多个道路温度设置来规避这个问题实际上是不可行的。
- 筒井等[218,217]在自然界中发现了一个很好的类比:个体的表型特征由其遗传密码描述。在解读这段代码的过程中,可能会出现体温异常、营养失衡、受伤、疾病等扰动。如果在这些影响下出现的表型特征具有低适应度,则有机体无法生存和繁殖。因此,如果其表型特征对扰动过于敏感,即使是具有良好遗传物质的物种也会灭绝。另一方面,抵抗它们的物种将生存和进化。
数学代写|优化算法作业代写optimisation algorithms代考|Countermeasures
对于问题空间对应于实向量的特殊情况(X⊆Rn),已经开发了几种处理鲁棒性问题的方法。受田口方法的启发6[209],可能的干扰由一个向量表示d=(d1,d2,…,dn)吨,d一世∈R在格雷纳的方法中[87,88]. 如果分布和影响d一世已知,目标函数F(X):X∈X可以改写为F~(X,d)[235].在特殊情况下d是正态分布的,这可以简化为F~((X1+d1,X2+d2,…,Xn+dn)吨). 然后对概率分布进行采样是有意义的d一些吨次并使用平均值F~(X,d)对于优化过程中的每个目标函数评估。在最优值的情况下是目标函数F已知,方程 3 可以最小化。这种方法也用于 Wiesmann 等人的工作中[234,235]并且基本上将优化算法变成了最大似然估计器之类的东西。
F′(X)=1吨∑一世=1吨(是−F¯(X,d一世))2
该方法对应于在目标函数评估期间使用多个不同的训练场景X⊈Rn. 通过向训练案例添加随机噪声和人工扰动,可以增加获得在噪声条件下应用或实现时稳定的稳健解决方案的机会。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
