如果你也在 怎样代写博弈论Game Theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
博弈论是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
statistics-lab™ 为您的留学生涯保驾护航 在代写博弈论Game Theory方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写博弈论Game Theory代写方面经验极为丰富,各种代写博弈论Game Theory相关的作业也就用不着说。
我们提供的博弈论Game Theory及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
经济代写|博弈论代写Game Theory代考|Evaluation of Heuristics
Our goal is to evaluate the heuristics we used to reduce the number of possible ways HPs can be allocated in the network to make the algorithm more scalable compared to our previous experiments. In the first experiment, we evaluate the solution quality of the algorithm with and without heuristics by comparing how early the defender can identify an attacker. We used different sizes of networks with different limits on the number of rounds the players can play. Each of the three attackers we considered, $a, b, c$, has some unique and some shared exploits in their possession. Attacker $a$ has exploits $\phi_{0}, \phi_{1}, \phi_{2}$. Attacker $b$ has exploits $\phi_{2}, \phi_{3}, \phi_{1}$. Attacker $c$ has exploits $\phi_{4}, \phi_{5}, \phi_{2}$. We picked the attacker $b$ as the acting attacker. We kept the edge density and shared vulnerabilities between nodes to $40 \%$. Results are averaged over 20 game instances. In the Figure $3.9$, the first row, Figure $3.9 \mathrm{a}$ and $\mathrm{b}$ computes the solution without using the heuristics and the second row, Figure $3.9 \mathrm{c}$ and d computes the solution using the heuristics to reduce the action space. As we can see, the solution quality did not degrade for the experiments we conducted. However, currently, we have no proof to guarantee an optimal solution with the use of heuristics.
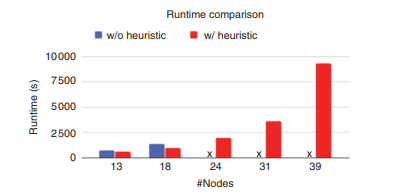
In the next experiment, we compare the run time between the algorithms using without and with heuristics for different sizes of networks and the same setup as the previous experiment. Run times are averaged over all the attackers for a particular size of games. As shown in Figure $3.10$, for smaller instances the algorithm with heuristics can compute the solution much quicker than if we do not use any heuristics. For larger instances of games if we do not heuristics, the algorithm runs out of memory very quickly (as shown by ” $x$ “), whereas using the heuristic we can compute the solutions.
经济代写|博弈论代写Game Theory代考|Conclusions and Future Direction
Identification of an attacker is an even harder problem in many ways than detection, especially when many attackers use similar TTP in the early stages of attacks. However, any information that can help to narrow down the intention and likely TTP of an attacker can also be of immense value to the defender if it is available early on.
We present several case studies and a formal game model showing how we can use deception techniques to identify different types of attackers represented by the different AGs they use in planning optimal attacks based on their individual goals and capabilities. We show that strategically using deception can facilitate significantly earlier identification by leading attackers to take different actions early in the attack that can be observed by the defender. Our simulation results show this in a more general setting. However, the optimal algorithm does not scale very well since it considers all the possible action space to allocate HPs. So, we presented a scalable version of the optimal algorithm that reduces the action space by a reasonable margin to handle larger instances of games. In future work, we plan to explore how this model can be extended to different types of deception strategies, integration with other IDS techniques, as well as larger and more diverse sets of possible attacker types to make it operational in the real world.
经济代写|博弈论代写Game Theory代考|Reward Function
As introduced earlier, there is a cost associated with each action. The network defender incurs a fixed cost for placing a new honeypot on an edge in the network. Let $P_{\mathrm{c}}$ denote the honeypot placement cost. On the attacker side, there is a cost per attack denoted as $A_{\mathrm{c}}$. The attack cost reflects the risk taken by the attacker as mentioned earlier.
If the defender placed honeypot on the same edge the attacker exploits, the defender gains a capturing reward. Otherwise, if the attacker exploited another safe edge, the attacker gains a successful attack reward. Let Cap and Esc denote the defender capture reward and the attacker successful reward, respectively.
To account for different nodes in the network, we adopt a reward function that takes into account the importance of the network nodes. Therefore, both capturing reward and the successful attack reward are weighted by the value of the secured or attacked node value, $w_{v}$. We start by expressing the reward matrix for the game illustrated in Figure $4.1$ and present the general reward matrix afterward.
$$
R_{1}=\left[\begin{array}{ccc}
-P_{\mathrm{c}}+A_{\mathrm{c}}+\operatorname{Cap} * w_{b} & -P_{\mathrm{c}}+A_{\mathrm{c}}-\operatorname{Esc} * w_{c} & -P_{\mathrm{c}} \
-P_{\mathrm{c}}+A_{\mathrm{c}}-\mathrm{Esc} * w_{\mathrm{b}} & -P_{\mathrm{c}}+A_{\mathrm{c}}+\operatorname{Cap} * w_{\mathrm{c}} & -P_{\mathrm{c}} \
A_{\mathrm{c}}-\operatorname{Esc} * w_{b} & A_{\mathrm{c}}-\mathrm{Esc} * w_{c} & 0
\end{array}\right] .
$$
The attacker reward matrix is $R_{2}=-R_{1}$. The reward, $R_{1}(1,1)$ and $R_{1}(2,2)$, represents a captured attacker as the defender installed a honeypot at the attacked node. Therefore, the defender pays placement cost $P_{\mathrm{c}}$ and gains a capturing reward weighted by the value of the defended node. The attacker incurs an attack cost, $A_{\mathrm{c}}$, which represents a reward for the defender in a zero-sum game. On the other hand, $R_{1}(1,2)$ and $R_{1}(2,1)$ represent a successful attack, where the honeypot is allocated at a different node. Therefore, there is a Esc loss weighted by the compromised node value. In $R_{1}(3,1)$ and $R_{1}(3,2)$, the defender decides not to place any honeypot to save placement
cost $P_{\mathrm{c}^{+}}$Similarly, in $R_{1}(1,3), R_{1}(2,3)$, and $R_{1}(3,3)$, the attacker backs off to either avoid capture cost or attack cost $A_{\mathrm{c}}$.
The reward function can easily be generalized to an arbitrary number of possible edges as follows.
$$
R_{1}\left(a_{1}, a_{2}\right)=\left{\begin{array}{clr}
-P_{\mathrm{c}}+A_{\mathrm{c}}+\operatorname{Cap} * w_{v} ; & a_{1}=e_{a, w}, a_{2}=v & \forall v \in \mathcal{V} \
-P_{\mathrm{c}}+A_{\mathrm{c}}-\mathrm{Esc} * w_{u} ; & a_{1}=e_{a, v}, a_{2}=u & \forall u \neq v \in \mathcal{V} \
-P_{\mathrm{c}} ; & a_{1}=e_{a, v}, a_{2}=0 & \forall v \in \mathcal{V} \
0 ; & a_{1}=0, a_{2}=0 &
\end{array}\right.
$$
where $a_{1}=0$ denotes the defender is not allocating any new honeypot. Similarly, $a_{2}=0$ denotes the attacker decided to back off.
博弈论代考
经济代写|博弈论代写Game Theory代考|Evaluation of Heuristics
我们的目标是评估我们用来减少在网络中分配 HP 的可能方式的数量的启发式方法,以使算法与我们之前的实验相比更具可扩展性。在第一个实验中,我们通过比较防御者可以多早识别攻击者来评估使用和不使用启发式算法的算法的解决方案质量。我们使用了不同规模的网络,对玩家可以玩的回合数有不同的限制。我们考虑的三个攻击者中的每一个,一个,b,C,拥有一些独特的和一些共同的功绩。攻击者一个有功绩φ0,φ1,φ2. 攻击者b有功绩φ2,φ3,φ1. 攻击者C有功绩φ4,φ5,φ2. 我们选择了攻击者b作为代理攻击者。我们保持节点之间的边缘密度和共享漏洞以40%. 结果平均超过 20 个游戏实例。图中3.9,第一行,图3.9一个和b在不使用启发式和第二行的情况下计算解决方案,图3.9Cd 使用启发式计算解决方案以减少动作空间。正如我们所看到的,我们进行的实验的解决方案质量没有下降。然而,目前,我们没有证据来保证使用启发式算法的最佳解决方案。
在下一个实验中,我们比较了在不同规模的网络和与前一个实验相同的设置下使用启发式算法和不使用启发式算法的算法之间的运行时间。对于特定规模的游戏,运行时间是所有攻击者的平均值。如图3.10,对于较小的实例,具有启发式算法的算法可以比不使用任何启发式算法更快地计算解决方案。对于更大的游戏实例,如果我们不进行启发式算法,算法会很快耗尽内存(如“X“),而使用启发式我们可以计算解决方案。
经济代写|博弈论代写Game Theory代考|Conclusions and Future Direction
在许多方面,识别攻击者比检测更难,尤其是当许多攻击者在攻击的早期阶段使用类似的 TTP 时。但是,任何有助于缩小攻击者意图和可能的 TTP 范围的信息,如果早期可用,对防御者来说也可能具有巨大价值。
我们提出了几个案例研究和一个正式的博弈模型,展示了我们如何使用欺骗技术来识别不同类型的攻击者,这些攻击者由他们根据个人目标和能力规划最佳攻击时使用的不同 AG 代表。我们表明,策略性地使用欺骗可以通过引导攻击者在攻击早期采取防御者可以观察到的不同行动来显着促进早期识别。我们的模拟结果在更一般的环境中显示了这一点。然而,最优算法不能很好地扩展,因为它考虑了所有可能的动作空间来分配 HP。因此,我们提出了优化算法的可扩展版本,该算法将动作空间减少了合理的余量,以处理更大的游戏实例。在以后的工作中,
经济代写|博弈论代写Game Theory代考|Reward Function
如前所述,每个动作都有相关的成本。网络防御者在网络边缘放置一个新的蜜罐会产生固定成本。让磷C表示蜜罐放置成本。在攻击者方面,每次攻击的成本表示为一个C. 如前所述,攻击成本反映了攻击者所承担的风险。
如果防御者将蜜罐放置在攻击者利用的同一边缘,则防御者将获得捕获奖励。否则,如果攻击者利用了另一个安全边缘,攻击者将获得成功的攻击奖励。令 Cap 和 Esc 分别表示防御者捕获奖励和攻击者成功奖励。
为了考虑网络中的不同节点,我们采用了考虑到网络节点重要性的奖励函数。因此,捕获奖励和成功攻击奖励均由受保护或被攻击节点的价值加权,在在. 我们首先表示如图所示游戏的奖励矩阵4.1然后给出一般的奖励矩阵。
R1=[−磷C+一个C+帽∗在b−磷C+一个C−Esc键∗在C−磷C −磷C+一个C−和sC∗在b−磷C+一个C+帽∗在C−磷C 一个C−Esc键∗在b一个C−和sC∗在C0].
攻击者奖励矩阵为R2=−R1. 奖励,R1(1,1)和R1(2,2), 代表被捕获的攻击者,因为防御者在受攻击的节点上安装了一个蜜罐。因此,防守方支付安置费用磷C并获得由防御节点的价值加权的捕获奖励。攻击者产生攻击成本,一个C,这表示在零和游戏中对防御者的奖励。另一方面,R1(1,2)和R1(2,1)代表一次成功的攻击,蜜罐被分配在不同的节点。因此,存在由受损节点值加权的 Esc 损失。在R1(3,1)和R1(3,2),防守方决定不放置任何蜜罐以保存放置
成本磷C+同样,在R1(1,3),R1(2,3), 和R1(3,3),攻击者后退以避免捕获成本或攻击成本一个C.
奖励函数可以很容易地推广到任意数量的可能边,如下所示。
$$
R_{1}\left(a_{1}, a_{2}\right)=\left{
−磷C+一个C+帽∗在在;一个1=和一个,在,一个2=在∀在∈在 −磷C+一个C−和sC∗在在;一个1=和一个,在,一个2=在∀在≠在∈在 −磷C;一个1=和一个,在,一个2=0∀在∈在 0;一个1=0,一个2=0\正确的。
$$
在哪里一个1=0表示防御者没有分配任何新的蜜罐。相似地,一个2=0表示攻击者决定后退。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
