如果你也在 怎样代写数据科学data science这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
数据科学是一个跨学科领域,它使用科学方法、流程、算法和系统从嘈杂的、结构化和非结构化的数据中提取知识和见解,并在广泛的应用领域应用数据的知识和可操作的见解。
statistics-lab™ 为您的留学生涯保驾护航 在代写数据科学data science方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写数据科学data science方面经验极为丰富,各种代写数据科学data science相关的作业也就用不着说。
我们提供的数据科学data science及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等楖率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
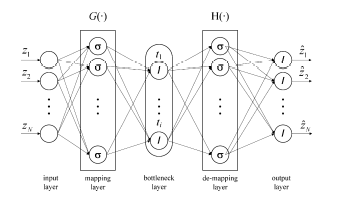
统计代写|数据科学代写data science代考|Principal curve and manifold approaches
Resulting from the fact that the nearest projection coordinate of each sample in the curve is searched along the whole line segments, the computational complexity of the HSPCs algorithm is of order $O\left(n^{2}\right)[25]$ which is dominated by the projection step. The HSPCs algorithm, as well as other algorithms proposed by $[4,18,19,69]$, may therefore be computationally expensive for large data sets.
For addressing the computational issue, several strategies are proposed in subsequently refinements. In reference [8], the $\mathrm{PPS}$ algorithm supposes that the data are generated from a collection of latent nodes in low-dimensional
space, and the computation to determine the projections is achieved by comparing the distances among data and the high-dimensional counterparts in the latent nodes. This results in a considerable reduction in the computational complexity if the number of the latent nodes is less than that number of observations. However, the PPS algorithm requires additional $O\left(N^{2} n\right)$ operations (Where $n$ is the dimension of latent space) to compute an orthonormalization. Hence, this algorithm is difficult to generalize in high-dimensional spaces.
In [73], local principal component analysis in each neighborhood is employed for searching a local segment. Therefore, the computational complexity is closely relate to the number of local PCA models. However, it is difficulty for general data to combine the segments into a principal curve because a large number of computational steps are involved in this combination.
For the work by Kégl $[34,35]$, the KPCs algorithm is proposed by combining the vector quantization with principal curves. Under the assumption that data have finite second moment, the computational complexity of the KPCs algorithm is $O\left(n^{5 / 3}\right)$ which is slightly less than that of the HSPCs algorithm. When allowing to add more than one vertex at a time, the complexity can be significantly decreased. Furthermore, a speed-up strategy discussed by Kégl [33] is employed for the assignments of projection indices for the data during the iterative projection procedure of the ACKPCs algorithms. If $\delta v^{(j)}$ is the maximum shift of a vertex $v_{j}$ in the $j$ th optimization step defined by:
$$
\delta v^{(j)}=\max {i=1, \cdots, k+1}\left|v{i}^{(j)}-v_{i}^{(j+1)}\right|,
$$
then after the $\left(j+j_{1}\right)$ optimization step, $s_{i_{1}}$ is still the nearest line segment to $x$ if
$$
d\left(x, s_{i_{1}}^{(j)}\right) \leq d\left(x, s_{i_{2}}^{(j)}\right)-2 \sum_{l=j}^{j+j_{1}} \delta v^{(l)}
$$
Further reference to this issue may be found in [33], pp. 66-68. Also, the stability of the algorithm is enhanced while the complexity is the equivalent to that of the KPCs algorithm.
统计代写|数据科学代写data science代考|Neural network approaches
The discussion in Subsect. $4.2$ highlighted that neural network approaches to determine a NLPCA model are difficult to train, particulary the 5 layer network by Kramer [37]. More precisely, the network complexity increases considerably if the number of original variables z,$N$, rises. On the other hand, an increasing number of observations also contribute to a drastic increase in the computational cost. Since most of the training algorithms are iterative in nature and employ techniques based on the backpropagation principle, for example the Levenberg-Marquardt algorithm for which the Jacobian matrix is updated using backpropagation, the performance of the identified network depends on the initial selection for the network weights. More precisely, it may
be difficult to determine a minimum for the associated cost function, that is the sum of the minimum distances between the original observations and the reconstructed ones.
The use of the IT network [68] and the approach by Dong and McAvoy [16] however, provide considerably simpler network topologies that are accordingly easier to train. Jia et al. [31] argued that the IT network can generically rep. resent smooth nonlinear functions and raised concern about the techniqu by Dong and McAvoy in terms of its flexibility in providing generic nonlin. ear functions. This concern related to to concept of incorporating a linea combinátion of nonlinear function to éstimate the nonlinear interrelationshipx between the recorded observations. It should be noted, however, that the IT network structure relies on the condition that an functional injective rela tionship exit bétween thé scorré variảblés and the original variảblés, that a unique mapping between the scores and the observations exist. Otherwise the optimization step to determine the scores from the observations using the identified IT network may converge to different sets of score values depending on the initial guess, which is undesirable. In contrast, the technique by Dong and McAvoy does not suffer from this problem.
统计代写|数据科学代写data science代考|Kernel PCA
In comparison to neural network approaches, the computational demand for a KPCA insignificantly increase for larger values of $N$, size of the original variables set $\mathbf{z}$, which follows from (1.59). In contrast, the size of the Gram matrix increases quadratically with a rise in the number of analyzed observations, $K$. However, the application of the numerically stable singular value decomposition to obtain the eigenvalues and eigenvectors of the Gram matrix does not present the same computational problems as those reported for the neural network approaches above.
数据可视化代写
统计代写|数据科学代写data science代考|Principal curve and manifold approaches
由于沿整个线段搜索曲线中每个样本的最近投影坐标,因此HSPCs算法的计算复杂度是有序的这(n2)[25]这是由投影步骤控制的。HSPCs 算法,以及由 HSPCs 提出的其他算法[4,18,19,69],因此对于大型数据集而言,计算成本可能很高。
为了解决计算问题,在随后的改进中提出了几种策略。在参考文献 [8] 中,磷磷小号算法假设数据是从低维潜在节点的集合中生成的
空间,确定投影的计算是通过比较数据和潜在节点中的高维对应物之间的距离来实现的。如果潜在节点的数量少于观察的数量,这将导致计算复杂度的显着降低。但是,PPS 算法需要额外的这(ñ2n)操作(其中n是潜在空间的维度)来计算正交归一化。因此,该算法难以在高维空间中泛化。
在[73]中,每个邻域的局部主成分分析用于搜索局部片段。因此,计算复杂度与局部 PCA 模型的数量密切相关。然而,一般数据很难将这些段组合成一条主曲线,因为这种组合涉及大量的计算步骤。
凯格尔的作品[34,35],将矢量量化与主曲线相结合,提出了KPCs算法。在数据具有有限二阶矩的假设下,KPCs 算法的计算复杂度为这(n5/3)略小于 HSPCs 算法。当允许一次添加多个顶点时,可以显着降低复杂性。此外,在 ACKPCs 算法的迭代投影过程中,采用 Kégl [33] 讨论的加速策略来分配数据的投影索引。如果d在(j)是顶点的最大位移在j在里面j优化步骤定义为:
d在(j)=最大限度一世=1,⋯,ķ+1|在一世(j)−在一世(j+1)|,
然后之后(j+j1)优化步骤,s一世1仍然是最近的线段X如果
d(X,s一世1(j))≤d(X,s一世2(j))−2∑l=jj+j1d在(l)
可以在 [33], pp. 66-68 中找到对该问题的进一步参考。此外,算法的稳定性得到了增强,而复杂度与 KPCs 算法相当。
统计代写|数据科学代写data science代考|Neural network approaches
小节中的讨论。4.2强调确定 NLPCA 模型的神经网络方法很难训练,特别是 Kramer [37] 的 5 层网络。更准确地说,如果原始变量 z 的数量,网络复杂度会显着增加,ñ, 上升。另一方面,越来越多的观察也导致计算成本的急剧增加。由于大多数训练算法本质上是迭代的并且采用基于反向传播原理的技术,例如使用反向传播更新雅可比矩阵的 Levenberg-Marquardt 算法,因此识别网络的性能取决于网络的初始选择权重。更准确地说,它可能
很难确定相关成本函数的最小值,即原始观测值与重建观测值之间的最小距离之和。
然而,使用 IT 网络 [68] 以及 Dong 和 McAvoy [16] 的方法提供了相当简单的网络拓扑,因此更容易训练。贾等人。[31] 认为 IT 网络通常可以代表。对平滑非线性函数感到不满,并对 Dong 和 McAvoy 的技术在提供通用非线性函数方面的灵活性提出了担忧。耳功能。这种关注与合并非线性函数的线性组合以估计记录的观测值之间的非线性相互关系x 的概念有关。然而,应该注意的是,IT 网络结构依赖于在 scorré variảblés 和原始变量之间存在函数单射关系的条件,即分数和观察值之间存在唯一的映射。否则,使用已识别的 IT 网络从观察中确定分数的优化步骤可能会根据初始猜测收敛到不同的分数值集,这是不希望的。相比之下,Dong 和 McAvoy 的技术则没有遇到这个问题。
统计代写|数据科学代写data science代考|Kernel PCA
与神经网络方法相比,KPCA 的计算需求对于较大的ñ, 原始变量集的大小和,从 (1.59) 得出。相反,Gram 矩阵的大小随着分析观察次数的增加呈二次方增加,ķ. 然而,应用数值稳定的奇异值分解来获得 Gram 矩阵的特征值和特征向量并不存在与上述神经网络方法所报道的计算问题相同的计算问题。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。统计代写|python代写代考
随机过程代考
在概率论概念中,随机过程是随机变量的集合。 若一随机系统的样本点是随机函数,则称此函数为样本函数,这一随机系统全部样本函数的集合是一个随机过程。 实际应用中,样本函数的一般定义在时间域或者空间域。 随机过程的实例如股票和汇率的波动、语音信号、视频信号、体温的变化,随机运动如布朗运动、随机徘徊等等。
贝叶斯方法代考
贝叶斯统计概念及数据分析表示使用概率陈述回答有关未知参数的研究问题以及统计范式。后验分布包括关于参数的先验分布,和基于观测数据提供关于参数的信息似然模型。根据选择的先验分布和似然模型,后验分布可以解析或近似,例如,马尔科夫链蒙特卡罗 (MCMC) 方法之一。贝叶斯统计概念及数据分析使用后验分布来形成模型参数的各种摘要,包括点估计,如后验平均值、中位数、百分位数和称为可信区间的区间估计。此外,所有关于模型参数的统计检验都可以表示为基于估计后验分布的概率报表。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
statistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
机器学习代写
随着AI的大潮到来,Machine Learning逐渐成为一个新的学习热点。同时与传统CS相比,Machine Learning在其他领域也有着广泛的应用,因此这门学科成为不仅折磨CS专业同学的“小恶魔”,也是折磨生物、化学、统计等其他学科留学生的“大魔王”。学习Machine learning的一大绊脚石在于使用语言众多,跨学科范围广,所以学习起来尤其困难。但是不管你在学习Machine Learning时遇到任何难题,StudyGate专业导师团队都能为你轻松解决。
多元统计分析代考
基础数据: $N$ 个样本, $P$ 个变量数的单样本,组成的横列的数据表
变量定性: 分类和顺序;变量定量:数值
数学公式的角度分为: 因变量与自变量
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
