如果你也在 怎样代写金融统计Financial Statistics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
金融统计是将经济物理学应用于金融市场。它没有采用金融学的规范性根源,而是采用实证主义框架。它包括统计物理学的典范,强调金融市场的突发或集体属性。经验观察到的风格化事实是这种理解金融市场的方法的出发点。
statistics-lab™ 为您的留学生涯保驾护航 在代写金融统计Financial Statistics方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写金融统计Financial Statistics代写方面经验极为丰富,各种代写金融统计Financial Statistics相关的作业也就用不着说。
我们提供的金融统计Financial Statistics及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
统计代写|金融统计代写Financial Statistics代考|Ways to overcome the identified problems
Insights into the strengths and weaknesses of Lundberg’s model stimulated a search for new lines of development. Two of them have branched out. First, numerous articles and monographs (see, e.g., $[167],[66],[7],[93]$ ) have published developments to weaken the technical assumptions of this model, addressing more complex probability mechanisms of insurance and using more sophisticated stochastic processes to model the risk reserve’s dynamics. Second is an attempt to reconsider the structural assumptions of Lundberg’s model by means of control theory. According to C. Philipson (see [156], p. 68), both these lines of development are based on the fundamental conception of the collective risk theory, which was created by Filip Lundberg.
The boundary between these two approaches is fuzzy. For example, the random walk model with two levels mentioned by H. Cramér in [41] is a sophistication of the traditional model of risk reserve. Therefore, it relates to the first branch of development mentioned previously. But the same model can be attributed to the second branch of development, since the upper barrier is a tool which automatically prevents the risk reserve from growing unduly.
Sharing the opinion of $\mathrm{K}$. Borch about the shortcomings of the theory of collective risks, as listed in points (i)-(iii) in Section 1.5.3.3, many experts believed the merger of the fundamental concept of Lundberg’s model with the methods of control theory is urgently needed in order to make it consistent with realities of the insurance business. The most important step was deemed by experts to be an introduction to the model of the possibility to change decisions once made.
For example, C. Philipson wrote (see [156], p. 59) that the risk premiums on which the tariff is built, called the applied risk premiums, themselves form random processes with discontinuous time parameters. Their trajectories are step functions in which each new step starts at a moment of change in the tariff rates. Additionally, if the security loading in the premiums is a product of the prediction of some measure of the variation of the risk premium, then we have a superposition of processes of a similar structure.
统计代写|金融统计代写Financial Statistics代考|Diffusion risk model: a useful auxiliary tool
Despite the intuitive transparency of Lundberg’s model, its results are not at all obvious. Thus, even in the simplest case of absence of migration of insureds and exponentially distributed interclaim intervals, when the claim arrival process is a homogeneous Poisson process, and when claim amounts are exponentially distributed, the expression for the probability of ruin within time $t$ written out in equality (C.3), is quite complex.
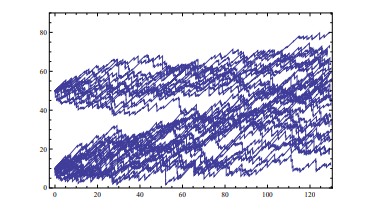
Looking at the trajectory of the risk reserve process from a considerable dis-
tance, we would see something similar to the trajectory of a Brownian motion with trend (see later shown Fig. 1.4). This suggests that the diffusion process can be used as a simplified model of the risk reserve process of an insurance company. At time $s \geqslant 0$, this model has the form
$$
R_{s}=u+c s-V_{s}, \quad V_{s}=\vartheta s+\sigma(\vartheta) \mathrm{W}{s+} $$ where, as before, $u$ denotes the initial capital, $c$ is the premium intensity otherwise simply known as price. The aggregate claim payments $V{s}, s \geqslant 0$, where $\mathrm{W}{s}, s \geqslant 0$, denotes a standard Wiener process, is a diffusion process starting at the origin and having drift parameter $\vartheta>0$ and diffusion parameter $\sigma(\vartheta)>0$. It is easy to see that $E V{s}=\vartheta s$ and $\mathrm{D} V_{s}=\sigma^{2}(\vartheta) s$. If the premium intensity $c$ is calculated according to the expected value principle ${ }^{76}$, i.e., if it is taken such that the mean aggregate claim payout and aggregate premiums collected are equal to each other, it equals $\vartheta$. If $c=\vartheta(1+\tau)$, then $\tau$ is called the premium loading.
Diffusion models are commonly used in risk theory for the following reasons. Firstly, when a more accurate description of the claim payout process is not required, these models are productive (see, e.g., [8], [192]). Secondly, if we approximate the jumping process of claim payments by a corresponding diffusion process, we may obtain useful approximation results for the original model (see, e.g., $[88],[78],[85],[183],[168],[73]$, and the survey work [6]). A number of useful results for the diffusion model (1.7) is gathered in Section C.1.
To explore diffusion model $(1.7)$ by analytical methods is easier, than Lundberg’s model, but when doing so, in addition to careful attention to the purely formal inconsistencies, such as the possibility of negative insurance payments ${ }^{77}$, a warning of restricted applicability, or non-applicability, should be clearly given.
统计代写|金融统计代写Financial Statistics代考|Program for building a model of long-term controlled insurance
In order to preserve the main advantages of Lundberg’s model and eliminate its main drawbacks described in Section 1.5.3, and in order to bring risk theory closer to the practical needs of insurance, we must move to a model of a multi-year controlled insurance process. This model is desirable as it reflects aspects such as reinsurance, investments, dividends, and bonuses.
Finnish and British Solvency Working Parties devised (see [53], Equation (1.1.1)) the following equation
$$
R^{[k \mid}=R^{|k-1|}+I^{[k]}+C^{|k|}+V_{\mathrm{re}}^{[k]}+A_{\text {new }}^{[k]}+B_{\text {new }}^{[k]}-V^{[k \mid}-E^{|k|}-I_{\mathrm{re}}^{|k|}-D^{|k|},
$$
as a year-to-year transition equation describing the dynamics of an insurance company from year to year. Here $k(k=1,2, \ldots)$ is the effective period’s, or account year’s, or simply year’s number, $R^{(k \mid}$ is the amount of assets at the end, and $R^{[k-1 \mid}$ at the beginning, of the $k$-th year, $I^{k \mid}$ is the premium income in the $k$-th year, $C^{|k|}$ is the return received in respect of the investments during the $k$-th year, $V_{r e}^{|k|}$ is the recovery from reinsurers during that period, $A_{\text {new }}^{\text {te }}$ is the new equity capital issued and subscribed for during that period, $B_{\text {new }}^{[k \mid}$ is the new debt capital issued and subscribed for during the $k$-th year and any other borrowing, $V^{|k|}$ is the amount of claim payments made during the $k$-th year including payments made on account, $E^{[k]}$ is the amount of commission paid and administration and operation expenses in the $k$-th year, $I_{\mathrm{re}}^{k]}$ is ceded reinsurance premium in the $k$-th year, and $D^{[k]}$ is the dividends paid to shareholders and bonuses paid to policyholders in the $k$-th year. Overall, all the variables, such as $R^{k \mid}$, $I^{|k|}$, etc., relate to the end of the $k$-th year.
Transition equation (1.8) describes the difference between all inflows, or revenues, and all outflows, or expenditures. Therefore, by its very nature, it is similar to equality (1.2). The obvious difference between the two of them is that the transition equation (1.8) reckons periods (insurance years), as it is usually done in the profit and loss accounting; traditional practice is that each accounting period ends by summarizing and making reports, and starts with developing administrative and control decisions ${ }^{78}$ on this basis.
金融统计代考
统计代写|金融统计代写Financial Statistics代考|Ways to overcome the identified problems
对 Lundberg 模型优缺点的洞察激发了对新发展路线的探索。其中两个已经分支出来。首先,大量的文章和专着(参见,例如,[167],[66],[7],[93]) 发表了削弱该模型的技术假设的进展,解决了更复杂的保险概率机制,并使用更复杂的随机过程来模拟风险准备金的动态。其次是试图通过控制理论重新考虑 Lundberg 模型的结构假设。根据 C. Philipson 的说法(参见 [156],第 68 页),这两条发展路线均基于 Filip Lundberg 创建的集体风险理论的基本概念。
这两种方法之间的界限是模糊的。例如,H.Cramér 在 [41] 中提到的具有两个级别的随机游走模型是传统风险准备金模型的复杂化。因此,它涉及到前面提到的第一个开发分支。但是同样的模型可以归因于第二个发展分支,因为上限是一种自动防止风险准备金过度增长的工具。
分享意见ķ. Borch 关于集体风险理论的缺点,如第 1.5.3.3 节 (i)-(iii) 中所列,许多专家认为,迫切需要将 Lundberg 模型的基本概念与控制理论方法相结合。使其与保险业务的实际情况相一致。专家认为最重要的一步是介绍一旦做出改变决定的可能性模型。
例如,C. Philipson 写道(参见 [156],第 59 页),建立关税的风险溢价称为应用风险溢价,它们本身形成具有不连续时间参数的随机过程。它们的轨迹是阶梯函数,其中每一个新步骤都从关税税率变化的时刻开始。此外,如果保费中的安全负载是对风险溢价变化的某种度量的预测的产物,那么我们就有类似结构的过程的叠加。
统计代写|金融统计代写Financial Statistics代考|Diffusion risk model: a useful auxiliary tool
尽管 Lundberg 的模型直观透明,但其结果并不明显。因此,即使在没有被保险人迁移和指数分布的索赔间隔的最简单情况下,当索赔到达过程是一个齐次泊松过程,并且当索赔金额呈指数分布时,时间内破产概率的表达式吨写在等式(C.3)中,是相当复杂的。
从一个相当大的角度来看风险准备金过程的轨迹
tance,我们会看到类似于带有趋势的布朗运动的轨迹(见后面的图 1.4)。这表明扩散过程可以作为保险公司风险准备金过程的简化模型。当时s⩾0, 这个模型有形式
Rs=在+Cs−在s,在s=ϑs+σ(ϑ)在s+和以前一样,在表示初始资本,C是溢价强度,也简称为价格。总索赔付款在s,s⩾0, 在哪里在s,s⩾0,表示标准维纳过程,是从原点开始并具有漂移参数的扩散过程ϑ>0和扩散参数σ(ϑ)>0. 很容易看出和在s=ϑs和D在s=σ2(ϑ)s. 如果溢价强度C是按照期望值原理计算的76,即,如果平均总索赔支出和收取的总保费彼此相等,则等于ϑ. 如果C=ϑ(1+τ), 然后τ称为溢价加载。
扩散模型通常用于风险理论,原因如下。首先,当不需要对索赔支付过程进行更准确的描述时,这些模型是有效的(例如,参见[8]、[192])。其次,如果我们通过相应的扩散过程来近似索赔支付的跳跃过程,我们可以获得原始模型的有用近似结果(参见,例如,[88],[78],[85],[183],[168],[73],以及调查工作[6])。扩散模型(1.7)的一些有用结果在 C.1 节中收集。
探索扩散模型(1.7)通过分析方法比 Lundberg 的模型更容易,但在这样做时,除了要仔细注意纯粹形式上的不一致,例如负保险支付的可能性77,应明确给出限制适用或不适用的警告。
统计代写|金融统计代写Financial Statistics代考|Program for building a model of long-term controlled insurance
为了保留 Lundberg 模型的主要优点并消除其在第 1.5.3 节中描述的主要缺点,并使风险理论更接近保险的实际需求,我们必须转向多年控制保险模型过程。该模型是可取的,因为它反映了再保险、投资、股息和奖金等方面。
芬兰和英国偿付能力工作组设计了(参见 [53],方程(1.1.1))以下方程
R[ķ∣=R|ķ−1|+我[ķ]+C|ķ|+在r和[ķ]+一个新的 [ķ]+乙新的 [ķ]−在[ķ∣−和|ķ|−我r和|ķ|−D|ķ|,
作为描述保险公司逐年动态的逐年过渡方程。这里ķ(ķ=1,2,…)是有效期间,或会计年度,或只是年份的数字,R(ķ∣是最后的资产数量,并且R[ķ−1∣在开始时,ķ- 年,我ķ∣是保费收入ķ- 年,C|ķ|是在投资期间收到的回报ķ- 年,在r和|ķ|是在此期间从再保险公司获得的恢复,一个新的 你 是在该期间发行和认购的新股本,乙新的 [ķ∣是期间发行和认购的新债务资本ķ- 第一年和任何其他借款,在|ķ|是索赔期间支付的金额ķ- 包括帐户付款在内的第 1 年,和[ķ]是支付的佣金和管理和运营费用的金额ķ- 年,我r和ķ]被分出的再保险费在ķ- 年,和D[ķ]是支付给股东的股息和支付给投保人的红利ķ- 年。总体而言,所有变量,例如Rķ∣, 我|ķ|等,与结尾有关ķ- 年。
转移方程(1.8)描述了所有流入或收入与所有流出或支出之间的差异。因此,就其本质而言,它类似于等式(1.2)。两者之间的明显区别在于,转换方程(1.8)计算期间(保险年度),就像在损益会计中通常所做的那样;传统做法是每个会计期间以总结和报告结束,并从制定行政和控制决策开始78以这个为基础。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
