如果你也在 怎样代写随机控制Stochastic Control这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
随机控制或随机最优控制是控制理论的一个子领域,它涉及到观察中或驱动系统演变的噪声中存在的不确定性。
随机控制或随机最优控制是控制理论的一个子领域,它涉及到观察中或驱动系统进化的噪声中存在的不确定性。系统设计者以贝叶斯概率驱动的方式假设,具有已知概率分布的随机噪声会影响状态变量的演变和观察。随机控制的目的是设计受控变量的时间路径,以最小的成本执行所需的控制任务,尽管存在这种噪声,但以某种方式定义。
statistics-lab™ 为您的留学生涯保驾护航 在代写随机控制Stochastic Control方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写随机控制Stochastic Control代写方面经验极为丰富,各种代写随机控制Stochastic Control相关的作业也就用不着说。
我们提供的随机控制Stochastic Control及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础

统计代写|随机控制代写Stochastic Control代考|Advances of Structural Control
Modern control theory was originally from the Wiener filter theory and the Wiener control theory in mid-twentieth century (Wiener 1948,1949 ). It became a fairly complete formulation through a rapid development in the subsequent 20 years. Beginning with the early of 1970 s, the deterministic optimal control and stochastic optimal control of structures have been developed into almost independent two branches.
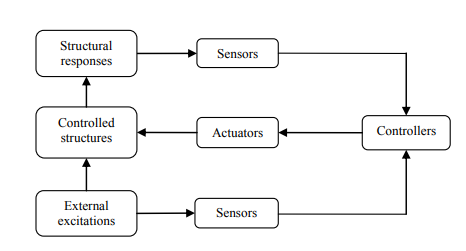
Structural control is devised to reduce or mitigate the responses of structures by utilizing the specified devices or facilities deployed in structures that are capable of shifting, dissipating, absorbing, and supplying energy. A diagram of typical logic of structural control is shown in Fig. 1.1. It is seen that a complete control system involves the sensor for monitoring the external excitation and the structural response, the controller for deducing the feedback law to regulate the structural state, and the actuator for implementing the control gain. According to whether a moderate power supply system is required for the operation of control system, structural control can be categorized into four modalities, i.e., the passive control, the active control, the semiactive control, and the hybrid control (Housner et al. 1997; Ou 2003; Teng 2009).
Passive control refers to a modality that allocates base isolation systems or energy dissipation devices to a structure so as to enhance the damping, stiffness, and strength of the structure. The control gain provided by passive systems just replies upon the structural response to the external excitation, and generally does not need power supplies. In early of 1970 s, Kelly and his colleagues proposed and experimentally proved the value of metal yield and energy dissipation component in the seismic mitigation of structures (Kelly et al. 1972; Skinner et al. 1975). The pioneering works played a significant role in the development of ductile design of seismic structures, which later formulated an important branch of structural control using energy dissipation schemes. Thereafter, an amount of energy dissipation components and devices were invented and applied into the vibration control of engineering structures under earthquakes and high winds, such as friction-type energy dissipation devices derived as the principle of automobile brakes (Pall and Marsh 1982; Li and Reinhorn 1995; Qu et al. 2001; Bhaskararao and Jangid 2006), viscoelastic dampers early used in the fatigue control of plane body (Zhang et al. 1989; Zhang and Soong 1992; Shen et al. 1995; Palmeri and Ricciardelli 2006; Xu 2007), viscous dampers or damping walls widely applied in the fields of military and aviation (Constantinou et al. 1993; Reinhorn et al. 1995; Museros and Martinez-Rodrigo 2007), tuned mass dampers (TMDs) and multiple-tuned mass dampers (MTMDs) (Villaverde 1994; Setareh 1994; Li 2000; Guo and Chen 2007; Wong and Johnson 2009), and tuned fluid dampers (Wakahara et al. 1992; Tamura et al. 1995; Tait et al. 2008). Until now, the research and development of energy dissipation devices with excellent performance are still one of the hotspot issues in the field of structural control (Chan and Albermani 2008; Jung et al. 2010; Zhang et al. 2013; Berardengo et al. 2015; Amjadian and Agrawal 2018).
统计代写|随机控制代写Stochastic Control代考|Stochastic Optimal Control of Structures
Since randomness inherent in the external excitations, the structural systems, and the control devices, the traditional deterministic control cannot guarantee the safety of structures. Stochastic optimal control of structures has thus become a challenging issue in the area of structural control (Housner et al. 1997). This topic can be traced back to the earlier researchers on the relevant fundamental theory. In 1940s, the stochastic differential theory had been established on the basis of the Itô calculus (Sobczyk 1991). Until to the late of 1950s and the early of 1960s, however, the development of the state-space method (Kalman 1960a), the maximum principle (Pontryagin 1962), the dynamic programming (Bellman 1957), and the Kalman-Bucy filtering theory (Kalman 1960b; Bucy and Kalman 1961) were eventually proposed and developed, which underlined the establishment of the modern optimal control theory. Stochastic optimal control then formed as a new branch of optimal control discipline.
统计代写|随机控制代写Stochastic Control代考|Classical Stochastic Optimal Control
The motivation of stochastic optimal control is to define the optimal control so that the transition probability density function (Spencer and Bergman 1993) or the statistical moments (Wojtkiewicz et al. 1996) are limited in a specified range of errors. In the theoretical framework of classical LQG control, there have formed the stochastic maximum principle (Yong and Zhou 1999) and the stochastic dynamic programming (Stengel 1994). Meanwhile, a series of design criteria for defining the stochastic optimal control law in accordance with the optimal control gain have been developed. The minimum variance criterion, for example, seeks for a control force with the objective of minimizing the variance of performance functions subjected to the mean constraint (Sain 1966). The optimal neighborhood feedback criterion involves an interaction scheme based on an initial costate estimation in view of the control equation and the performance objective (Stengel 1994). The statistical moment assessment criterion seeks for an optimal control law in the sense of trade-off, between the statistics of quantities of concern (Zhang and Xu 2001). The reliability-based design criterion is to attain a control law leading to a minimum failure probability of structural systems, through iteratively solving the limit state equation pertaining to the performance objective (Spencer et al. 1994a; May and Beck 1998). The probability density tracking criterion employs the Markov process theory to attain the analytical solution
of probability density of a family of specified systems, so as to define the control law approaching the desired probability density (Elbeyli and Sun 2002; Elbeyli et al. 2005; Sun 2006).
In aspect of stochastic optimal control of linear systems, the present moment reliability-based structural optimal control has a wide application. For example, Spencer et al. addressed the design and optimization method of a single-degreeof-freedom system attached with active tendon systems. In their work, a performance function directly relevant to the failure probability was defined, and the firstcrossing principle and a stationary white noise model of seismic ground motions were employed. Utilizing the first-order reliability method/the second-order reliability method (FORM/SORM), the reliability-based control of structures was then implemented so as to minimize the failure probability of structural displacement (Spencer et al. 1994a). Battaini et al. further employed the FORM/SORM to carry out the reliability assessment and experimental analysis of a controlled multi-degreeof-freedom system (Battaini et al. 2000). It was indicated in their work that the computational efficiency of moment-based reliability method was better than the Monte Carlo simulation, while the former merely attained an approximate solution in the case that the performance function of structures featured a high nonlinearity in the neighborhood of checking point, or that the distribution of basic random variables was far from the Gaussian distribution. The non-Gaussian properties of structural response might enlarge the error between the approximate solution and the accurate solution due to the high-order nonlinear mapping from the basic random variables to the structural responses. Therefore, the moment-based reliability method cannot be extended into the large-scale and complex structural systems. In 1998, May and Beck explored the first generation of Benchmark model pertaining to the probabilistic control problem, so as to maximize the reliability of the uncertain structures and control systems subjected to seismic ground motions. In this work, an acceleration feedback control scheme was employed aiming at the design of optimal active mass damper; the performance measure on the design objective includes the interstory drift, story acceleration of structures, and the deployment positions of sensors. An approximate expansion estimating the failure probability of structures was then proposed based on the level-crossing process theory (May and Beck 1998). However, their work involved the search iterations of the optimal value with respect to the approximate expansion and of the stochastic optimal control law, which will result in an increased computational cost.
随机控制代写
统计代写|随机控制代写Stochastic Control代考|Advances of Structural Control
现代控制理论起源于维纳滤波器理论和二十世纪中叶的维纳控制理论(Wiener 1948,1949)。在随后的 20 年中经过快速发展,形成了较为完整的配方。从1970年代初开始,结构的确定性最优控制和随机最优控制已经发展成为几乎独立的两个分支。
结构控制旨在通过利用部署在能够转移、耗散、吸收和供应能量的结构中的指定设备或设施来减少或减轻结构的响应。结构控制的典型逻辑示意图如图 1.1 所示。可以看出,一个完整的控制系统包括用于监测外部激励和结构响应的传感器、用于推导反馈律以调节结构状态的控制器以及用于实现控制增益的执行器。根据控制系统运行是否需要适度的供电系统,结构控制可分为被动控制、主动控制、半主动控制和混合控制四种模式(Housner et al. 1997 ; 欧 2003; 滕 2009)。
被动控制是指将基础隔离系统或能量耗散装置分配给结构以增强结构的阻尼、刚度和强度的一种方式。无源系统提供的控制增益仅依赖于结构对外部激励的响应,一般不需要电源。1970 年代初,Kelly 和他的同事提出并通过实验证明了金属屈服和能量耗散分量在结构抗震中的价值(Kelly 等 1972;Skinner 等 1975)。这些开创性的工作在抗震结构延性设计的发展中发挥了重要作用,后来形成了使用能量耗散方案的结构控制的一个重要分支。此后,和调谐流体阻尼器(Wakahara et al. 1992; Tamura et al. 1995; Tait et al. 2008)。直到现在,性能优异的消能装置的研发仍然是结构控制领域的热点问题之一(Chan and Albermani 2008; Jung et al. 2010; Zhang et al. 2013; Berardengo et al. 2015 ; Amjadian 和 Agrawal 2018)。
统计代写|随机控制代写Stochastic Control代考|Stochastic Optimal Control of Structures
由于外部激励、结构系统和控制装置固有的随机性,传统的确定性控制无法保证结构的安全性。因此,结构的随机最优控制已成为结构控制领域的一个具有挑战性的问题(Housner et al. 1997)。这个话题可以追溯到早期研究人员对相关基础理论的研究。1940 年代,随机微分理论建立在伊藤演算的基础上(Sobczyk 1991)。然而,直到 1950 年代末和 1960 年代初,状态空间方法 (Kalman 1960a)、最大值原理 (Pontryagin 1962)、动态规划 (Bellman 1957) 和 Kalman-Bucy 滤波理论的发展(Kalman 1960b;Bucy 和 Kalman 1961)最终被提出和发展,强调了现代最优控制理论的建立。随机最优控制随后形成为最优控制学科的一个新分支。
统计代写|随机控制代写Stochastic Control代考|Classical Stochastic Optimal Control
随机最优控制的动机是定义最优控制,以使转移概率密度函数 (Spencer and Bergman 1993) 或统计矩 (Wojtkiewicz et al. 1996) 限制在指定的误差范围内。在经典 LQG 控制的理论框架中,形成了随机最大值原理(Yong and Zhou 1999)和随机动态规划(Stengel 1994)。同时,制定了一系列根据最优控制增益定义随机最优控制律的设计准则。例如,最小方差标准寻求一种控制力,其目标是使受到平均约束的性能函数的方差最小化(Sain 1966)。考虑到控制方程和性能目标(Stengel 1994),最优邻域反馈准则涉及基于初始共态估计的交互方案。统计矩评估标准在关注量的统计数据之间寻求权衡意义上的最优控制律(Zhang and Xu 2001)。基于可靠性的设计准则是通过迭代求解与性能目标相关的极限状态方程,获得导致结构系统故障概率最小的控制律(Spencer 等人 1994a;May 和 Beck 1998)。概率密度跟踪准则采用马尔可夫过程理论来获得解析解 统计矩评估标准在关注量的统计数据之间寻求权衡意义上的最优控制律(Zhang and Xu 2001)。基于可靠性的设计准则是通过迭代求解与性能目标相关的极限状态方程,获得导致结构系统故障概率最小的控制律(Spencer 等人 1994a;May 和 Beck 1998)。概率密度跟踪准则采用马尔可夫过程理论来获得解析解 统计矩评估标准在关注量的统计数据之间寻求权衡意义上的最优控制律(Zhang and Xu 2001)。基于可靠性的设计准则是通过迭代求解与性能目标相关的极限状态方程,获得导致结构系统故障概率最小的控制律(Spencer 等人 1994a;May 和 Beck 1998)。概率密度跟踪准则采用马尔可夫过程理论来获得解析解 通过迭代求解与性能目标相关的极限状态方程(Spencer et al. 1994a; May and Beck 1998)。概率密度跟踪准则采用马尔可夫过程理论来获得解析解 通过迭代求解与性能目标相关的极限状态方程(Spencer et al. 1994a; May and Beck 1998)。概率密度跟踪准则采用马尔可夫过程理论来获得解析解
一组特定系统的概率密度,从而定义接近所需概率密度的控制律(Elbeyli 和 Sun 2002;Elbeyli 等人 2005;Sun 2006)。
在线性系统的随机最优控制方面,基于矩可靠性的结构最优控制具有广泛的应用。例如,斯宾塞等人。研究了附有主动肌腱系统的单自由度系统的设计和优化方法。在他们的工作中,定义了与失效概率直接相关的性能函数,并采用了第一交叉原理和地震地面运动的静止白噪声模型。利用一阶可靠度法/二阶可靠度法(FORM/SORM),对结构进行基于可靠度的控制,以尽量减少结构位移的失效概率(Spencer et al. 1994a)。巴泰尼等人。进一步使用 FORM/SORM 进行受控多自由度系统的可靠性评估和实验分析(Battaini 等人,2000 年)。他们的工作表明,基于矩的可靠性方法的计算效率优于蒙特卡洛模拟,而前者只是在结构性能函数在校核附近具有高度非线性的情况下获得了近似解。点,或者基本随机变量的分布远离高斯分布。由于从基本随机变量到结构响应的高阶非线性映射,结构响应的非高斯特性可能会扩大近似解和精确解之间的误差。所以,基于力矩的可靠度方法不能推广到大型复杂的结构系统中。1998 年,May 和 Beck 探索了与概率控制问题有关的第一代 Benchmark 模型,以最大限度地提高受地震地震动影响的不确定结构和控制系统的可靠性。在这项工作中,针对优化主动质量阻尼器的设计,采用加速度反馈控制方案;设计目标的性能测量包括层间漂移、结构的层加速度和传感器的部署位置。然后基于水平交叉过程理论(May and Beck 1998)提出了估计结构失效概率的近似扩展。然而,
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
