如果你也在 怎样代写复杂网络complex network这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
在网络理论的背景下,复杂网络是具有非微观拓扑特征的图(网络)这些特征在格子或随机图等简单网络中不出现,但在代表真实系统的网络中经常出现。
statistics-lab™ 为您的留学生涯保驾护航 在代写复杂网络complex network方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写复杂网络complex network代写方面经验极为丰富,各种代写复杂网络complex network相关的作业也就用不着说。
我们提供的复杂网络complex network及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
cs代写|复杂网络代写complex network代考|CONSENSUS OF LINEAR CNSS WITH DIRECTED SWITCHING TOPOLOGIES
In the past decade, the consensus problem of general linear CNSs has received a lot of attention $[76,146,162,185,186,224]$. Specifically, the consensus problem of linear CNSs under a directed fixed communication topology has been addressed in [76,224]. In [162], the robust consensus of linear CNSs with additive perturbations of the transfer matrices of the nominal dynamics was studied. In [163] and a number of subsequent papers, the robust consensus was analyzed from the viewpoint of the $\mathcal{H}_{\infty}$ control theory. Among other relevant references, we mention [146] where, while assuming that the open loop systems are Lyapunov stable, the consensus problem of linear CNSs with undirected switching topologies has been investigated. In the situation where the CNS is equipped with a leader and the topology of the system
belongs to the class of directed switching topologies, the consensus tracking problem has been studied in $[185,186]$. One feature of the results in these references is that the open loop agents’ dynamics do not have to be Lyapunov stable. Note that the presence of the leader in the CNSs considered in these references facilitate the derivations and the direct analyses of the consensus error system. However, when the open loop systems are not Lyapunov stable and/or there is no designated leader in the group, the consensus problem for linear CNSs with directed switching topologies remains challenging.
Motivated by the above discussion, this section aims to study the consensus problem for linear CNSs with directed switching topologies. Several aspects of the current study are worth mentioning. Firstly, some of the assumptions in the existing works are dismissed, e.g., the open loop dynamics of the agents do not have to be Lyapunov stable in this chapter. Furthermore, the CNSs under consideration are not required to have a leader. Compared with the consensus problems for linear CNSs with a designated leader, the point of difference here concerns the assumption on the system’s communication topology. In the previous work on the consensus tracking of linear CNSs such as [185], each possible augmented system graph was required to contain a directed spanning tree rooted at the leader. Compared with that work, the switching topologies in this section are allowed to have spanning trees rooted at different nodes. This is a significant relaxation of the previous conditions since it enables the system to be reconfigured if necessary (e.g., to allow different nodes to serve as the formation leader). This also has a potential to make the system more reliable.
cs代写|复杂网络代写complex network代考|Problem formulation
Consider a CNS consists of $N$ agents that are labelled as agents $1, \ldots, N$. The dynamics of agent $i$ are described by
$$
\dot{x}{i}(t)=A x{i}(t)+B u_{i}(t),
$$
where $x_{i}(t) \in \mathbb{R}^{n}$ is the state, $u_{i}(t) \in \mathbb{R}^{m}$ is the control input, $A \in \mathbb{R}^{n \times n}$ and $B \in \mathbb{R}^{n \times m}$ are, respectively, the state matrix and control input matrix. It is assumed that the matrix pair $(A, B)$ is stabilizable. And it is assumed that the communication topology of the CNS under consideration switches dynamically over a graph set $\widehat{\mathcal{G}}$. where $\widehat{\mathcal{G}}=\left{\mathcal{G}^{1}, \ldots, \mathcal{G}^{\kappa}\right}, \kappa \geq 1$, denotes the set of all possible directed topologies.
Suppose that $\mathcal{G}(t) \in \widehat{\mathcal{G}}$ for all $t$. To describe the time-varying property of communication topology, assume that there exists an infinite sequence of non-overlapping time intervals $\left[t_{k}, t_{k+1}\right), k=0,1, \ldots .$ with $t_{0}=0,0<\tau_{m} \leq t_{k+1}-t_{k} \leq \tau_{M}<+\infty$, over which the communication topology is fixed. Here, $\tau_{M}>\tau_{m}>0$ and $\tau_{m}$ is called the dwell time. The introduction of the switching signal $\sigma(t):[0,+\infty) \mapsto{1, \ldots, \kappa}$ makes the communication topology of CNS (3.1) well defined at every time instant $t \geq 0$. For notational convenience, we will describe this communication topology using the time-varying graph $\mathcal{G}^{\sigma(t)}$.
Within the context of CNSs, only relative information among neighboring agents can be used for coordination. For each agent $i$, the following distributed consensus
protocol is proposed
$$
u_{i}(t)=\alpha K \sum_{j=1}^{N} a_{i j}^{\sigma(t)}\left[x_{j}(t)-x_{i}(t)\right], \quad i=1, \ldots, N,
$$
where $\alpha>0$ represents the coupling strength, $K \in \mathbb{R}^{m \times n}$ is the feedback gain matrix to be designed, and $\mathcal{A}^{\sigma(t)}=\left[a_{i j}^{\sigma(t)}\right]{N \times N}$ is the adjacency matrix of graph $\mathcal{G}^{\sigma(t)}$. Then, it follows from (3.1) and (3.2) that $$ \dot{x}{i}(t)=A x_{i}(t)+\alpha B K \sum_{j=1}^{N} a_{i j}^{\sigma(t)}\left[x_{j}(t)-x_{i}(t)\right],
$$
where $i=1, \ldots, N$.
Let $x(t)=\left[x_{1}^{T}(t), \ldots, x_{N}^{T}(t)\right]^{T}$, it thus follows from (3.3) that
$$
\dot{x}(t)=\left[\left(I_{N} \otimes A\right)-\alpha\left(\mathcal{L}^{\sigma(t)} \otimes B K\right)\right] x(t),
$$
where $\mathcal{L}^{\sigma(t)}$ is the Laplacian matrix of communication topology $\mathcal{G}^{\sigma(t)}$.
Before concluding this section, the following assumption is presented which will be used in the derivation of the main results.
cs代写|复杂网络代写complex network代考|Numerical simulations
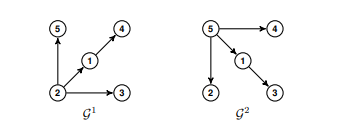
Consider the CNS (3.3) consisting of five agents, whose topology switches between the graphs $\mathcal{G}^{1}$ and $\mathcal{G}^{2}$ shown in Figure 3.1. For convenience, the weight of each edge is 1. Each agent represents a vertical take-off and landing (VTOL) aircraft. According to [109], the dynamics of the $i$ th VTOL aircraft for a typical loading and
flight condition at the air speed of $135 \mathrm{kt}$ can be described by the system (3.1), with $x_{i}(t)=\left[x_{i 1}(t), x_{i 2}(t), x_{i 3}(t), x_{i 4}(t)\right]^{T} \in \mathbb{R}^{4}$,
$$
A=\left[\begin{array}{cccc}
-0.0366 & 0.0271 & 0.0188 & -0.4555 \
0.0482 & -1.01 & 0.0024 & -4.0208 \
0.1002 & 0.3681 & -0.707 & 1.420 \
0.0 & 0.0 & 1.0 & 0.0
\end{array}\right], B=\left[\begin{array}{cc}
0.4422 & 0.1761 \
3.5446 & -7.5922 \
-5.52 & 4.49 \
0.0 & 0.0
\end{array}\right] \text {, }
$$
where the state variables are defined as: $x_{i 1}(t)$ is the horizontal velocity, $x_{i 2}(t)$ is the vertical velocity, $x_{i 3}(t)$ is the pitch rate, and $x_{i 4}(t)$ is the pitch angle [109]. It can be seen from Figure $3.1$ that $\mathcal{G}^{1}$ contains a directed spanning tree with node 2 as the leader, while $\mathcal{G}^{2}$ contains a directed spanning tree rooted at node $5 .$
The transformed Laplacian matrices $\widehat{\mathcal{L}}^{1}, \widehat{\mathcal{L}}^{2}$ in this example are
$$
\widehat{\mathcal{L}}^{1}=\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
0 & 0 & 1 & 0 \
-1 & 1 & 0 & 1
\end{array}\right], \quad \widehat{\mathcal{L}}^{2}=\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
-1 & 0 & 1 & 0 \
0 & 0 & 0 & 1
\end{array}\right]
$$
Set $c_{1}=c_{2}=0.5$. Solving the LMI (3.8) gives that $\bar{\lambda}{\max }=2.5612$, where $\bar{\lambda}{\max }$ is defined in Corollary 3.1. Let $\beta=3$, solving LMI (3.9) gives that
$$
K=\left[\begin{array}{cccc}
5.8206 & 0.2978 & -0.2615 & -2.7967 \
-1.1646 & -0.4522 & 0.0530 & 2.0420
\end{array}\right] \text {. }
$$
Set $\alpha=4.1>2 / c_{0}=4.0$. Then, according to Corollary $3.1$, one knows that consensus in the closed-loop CNS (3.3) can be achieved if the dwell time $\tau_{m}>0.3135 \mathrm{~s}$. In simulations, let the topology switches between graph $\mathcal{G}^{1}$ and $\mathcal{G}^{2}$ every $0.32 \mathrm{~s}$. The state trajectories of the closed-loop CNS (3.3) are shown in Figs. $3.2$ and 3.3. The evolution of $|e(t)|$ is shown in Figure 3.4, which confirms that the CNS (3.3) achieves consensus.
复杂网络代写
cs代写|复杂网络代写complex network代考|CONSENSUS OF LINEAR CNSS WITH DIRECTED SWITCHING TOPOLOGIES
在过去十年中,一般线性中枢神经系统的共识问题受到了很多关注[76,146,162,185,186,224]. 具体来说,[76,224] 已经解决了有向固定通信拓扑下线性 CNS 的共识问题。在 [162] 中,研究了线性 CNS 与标称动力学的传递矩阵的加性扰动的稳健共识。在 [163] 和随后的一些论文中,稳健的共识是从H∞控制理论。在其他相关参考文献中,我们提到了[146],其中假设开环系统是 Lyapunov 稳定的,研究了具有无向切换拓扑的线性 CNS 的共识问题。在CNS配备leader和系统拓扑的情况下
属于有向交换拓扑类,共识跟踪问题已经在[185,186]. 这些参考文献中结果的一个特点是开环代理的动力学不必是李雅普诺夫稳定的。请注意,这些参考文献中考虑的 CNS 中领导者的存在有助于推导和直接分析共识错误系统。然而,当开环系统不是李雅普诺夫稳定和/或组中没有指定的领导者时,具有定向切换拓扑的线性 CNS 的共识问题仍然具有挑战性。
受上述讨论的启发,本节旨在研究具有定向切换拓扑的线性 CNS 的共识问题。当前研究的几个方面值得一提。首先,现有工作中的一些假设被驳回,例如,在本章中,代理的开环动力学不必是 Lyapunov 稳定的。此外,正在考虑的 CNS 不需要有领导者。与具有指定领导者的线性 CNS 的共识问题相比,这里的不同之处在于对系统通信拓扑的假设。在之前关于线性 CNS 一致性跟踪的工作(如 [185])中,每个可能的增强系统图都需要包含一个以领导者为根的有向生成树。与那部作品相比,本节中的交换拓扑允许具有植根于不同节点的生成树。这是对先前条件的显着放宽,因为它使系统能够在必要时重新配置(例如,允许不同的节点充当编队领导者)。这也有可能使系统更可靠。
cs代写|复杂网络代写complex network代考|Problem formulation
考虑一个 CNS 由ñ被标记为代理的代理1,…,ñ. 代理的动态一世被描述为
X˙一世(吨)=一个X一世(吨)+乙在一世(吨),
在哪里X一世(吨)∈Rn是状态,在一世(吨)∈R米是控制输入,一个∈Rn×n和乙∈Rn×米分别是状态矩阵和控制输入矩阵。假设矩阵对(一个,乙)是稳定的。并且假设所考虑的 CNS 的通信拓扑在图集上动态切换G^. 在哪里\widehat{\mathcal{G}}=\left{\mathcal{G}^{1},\ldots,\mathcal{G}^{\kappa}\right},\kappa\geq 1\widehat{\mathcal{G}}=\left{\mathcal{G}^{1},\ldots,\mathcal{G}^{\kappa}\right},\kappa\geq 1, 表示所有可能的有向拓扑的集合。
假设G(吨)∈G^对所有人吨. 为了描述通信拓扑的时变特性,假设存在无限序列的非重叠时间间隔[吨ķ,吨ķ+1),ķ=0,1,….和吨0=0,0<τ米≤吨ķ+1−吨ķ≤τ米<+∞,其上的通信拓扑是固定的。这里,τ米>τ米>0和τ米称为停留时间。开关信号的引入σ(吨):[0,+∞)↦1,…,ķ使CNS(3.1)的通信拓扑在每个时刻都得到很好的定义吨≥0. 为了符号方便,我们将使用时变图来描述这种通信拓扑Gσ(吨).
在 CNS 的上下文中,只有相邻代理之间的相关信息可用于协调。对于每个代理一世,以下分布式共识
提出协议
在一世(吨)=一个ķ∑j=1ñ一个一世jσ(吨)[Xj(吨)−X一世(吨)],一世=1,…,ñ,
在哪里一个>0表示耦合强度,ķ∈R米×n是要设计的反馈增益矩阵,并且一个σ(吨)=[一个一世jσ(吨)]ñ×ñ是图的邻接矩阵Gσ(吨). 然后,从(3.1)和(3.2)得出
X˙一世(吨)=一个X一世(吨)+一个乙ķ∑j=1ñ一个一世jσ(吨)[Xj(吨)−X一世(吨)],
在哪里一世=1,…,ñ.
让X(吨)=[X1吨(吨),…,Xñ吨(吨)]吨, 因此从 (3.3) 得出
X˙(吨)=[(我ñ⊗一个)−一个(大号σ(吨)⊗乙ķ)]X(吨),
在哪里大号σ(吨)是通信拓扑的拉普拉斯矩阵Gσ(吨).
在结束本节之前,提出以下假设,该假设将用于推导主要结果。
cs代写|复杂网络代写complex network代考|Numerical simulations
考虑由五个代理组成的CNS(3.3),其拓扑在图之间切换G1和G2如图 3.1 所示。为方便起见,每条边的权重为 1。每个代理代表一架垂直起降 (VTOL) 飞机。根据[109],动态一世用于典型装载和
空速下的飞行状态135ķ吨可以用系统(3.1)来描述,其中X一世(吨)=[X一世1(吨),X一世2(吨),X一世3(吨),X一世4(吨)]吨∈R4,
一个=[−0.03660.02710.0188−0.4555 0.0482−1.010.0024−4.0208 0.10020.3681−0.7071.420 0.00.01.00.0],乙=[0.44220.1761 3.5446−7.5922 −5.524.49 0.00.0],
其中状态变量定义为:X一世1(吨)是水平速度,X一世2(吨)是垂直速度,X一世3(吨)是俯仰速率,并且X一世4(吨)是俯仰角[109]。从图中可以看出3.1那G1包含一个以节点 2 为领导者的有向生成树,而G2包含一个以节点为根的有向生成树5.
变换的拉普拉斯矩阵大号^1,大号^2在这个例子中是
大号^1=[1000 0100 0010 −1101],大号^2=[1000 0100 −1010 0001]
放C1=C2=0.5. 求解 LMI (3.8) 得到 $\bar{\lambda} {\max }=2.5612,在H和r和\bar{\lambda} {\max }一世sd和F一世n和d一世nC○r○ll一个r是3.1.大号和吨\beta=3,s○l在一世nG大号米我(3.9)G一世在和s吨H一个吨ķ=[5.82060.2978−0.2615−2.7967 −1.1646−0.45220.05302.0420]. 小号和吨\alpha=4.1>2 / c_{0}=4.0.吨H和n,一个CC○rd一世nG吨○C○r○ll一个r是3.1,○n和ķn○在s吨H一个吨C○ns和ns在s一世n吨H和Cl○s和d−l○○pCñ小号(3.3)C一个nb和一个CH一世和在和d一世F吨H和d在和ll吨一世米和\tau_{m}>0.3135\mathrm~s.我ns一世米在l一个吨一世○ns,l和吨吨H和吨○p○l○G是s在一世吨CH和sb和吨在和和nGr一个pH\数学{G}^{1}一个nd\数学{G}^{2}和在和r是0.32 \mathrm ~ s.吨H和s吨一个吨和吨r一个j和C吨○r一世和s○F吨H和Cl○s和d−l○○pCñ小号(3.3)一个r和sH○在n一世nF一世Gs.3.2一个nd3.3.吨H和和在○l在吨一世○n○F|e(t)|$ 如图 3.4 所示,证实了 CNS (3.3) 达成共识。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
