如果你也在 怎样代写机器学习machine learning这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
机器学习(ML)是人工智能(AI)的一种类型,它允许软件应用程序在预测结果时变得更加准确,而无需明确编程。机器学习算法使用历史数据作为输入来预测新的输出值。
statistics-lab™ 为您的留学生涯保驾护航 在代写机器学习machine learning方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写机器学习machine learning代写方面经验极为丰富,各种代写机器学习machine learning相关的作业也就用不着说。
我们提供的机器学习machine learning及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
cs代写|机器学习代写machine learning代考|Introduction
This chapter provides a high-level overview of machine learning, in particular of how it is related to building models from data. We start with a basic idea in the historical context and phrase the learning problem in a simple mathematical term as function approximation as well as in a probabilistic context. In contrast to more traditional models we can characterize machine learning as nonlinear regression in high-dimensional spaces. This chapter seeks to point out how diverse sub-areas such as deep learning and Bayesian networks fit into the scheme of things and aims to motivate the further study with some examples of recent progress.
Machine learning is literally about building machines, often in software, that can learn to perform specific tasks. Examples of common tasks for machine learning is recognizing objects from digital pictures or predicting the location of a robot or a selfdriving car from a variety of sensor measurements. These techniques have contributed largely to a new wave of technologies that are commonly associated with artificial intelligence (AI). This books is dedicated to introducing the fundamentals of this discipline.
The recent importance of machine learning and its rapid development with new industrial applications has been breath taking, and it is beyond the scope of this book to anticipate the multitude of developments that will occur. However, the knowledge of basic ideas behind machine learning, many of which have been around for some time, and their formalization for building probabilistic models to describe data are now important basic skills. Machine learning is about modeling data. Describing data and uncertainty has been the traditional domain of Bayesian statistics and probability theory. In contrast, it seems that many exciting recent techniques come from an area now called deep learning. The specific contribution of this book is its attempt to highlight the relationship between these areas.
We often simply say that we learn from data, but it is useful to realize that data can mean several things. In its most fundamental form, data usual consist of measurements such as intensity of light in a digital camera, the measurement of electric potentials in Electroencephalography (EEG), or the recording of stock-market data. However, what we need for learning is a teacher who provides us with information about what these data should predict. Such information can take many different forms. For example, we might have a form of data that we call labels, such as the identity of objects in a digital photograph. This is exactly the kind of information we need to learn optical object recognition. The teacher provides examples of the desired answers that the student (learner) should learn to predict for novel inputs.
cs代写|机器学习代写machine learning代考|Mathematical formulation of the basic learning problem
Much of what is currently most associated with the success of machine learning is supervised learning, sometimes also called predictive learning. The basic task of supervised learning is that of taking a collection of input data $x$, such as the pixel values of an image, measured medical data, or robotic sensor data, and predicting an output value $y$ such as the name of an object in an image, the state of a patient’s health, or the location of obstacles. It is common that each input has many components, such as many millions of pixel values in an image, and it is useful to collect these values in a mathematical structure such as a vectors (1-dimensional), a matrix (2-dimensional), or a tensor that is the generalization of such structures to higher dimensions. We often refer to machine learning problems as high-dimensional which refers, in this context, to the large number of components in the input structure and not to the dimension of the input tensor.
We use the mathematical terms vector, matrix, and tensor mainly to signify a data structure. In a programming context these are more commonly described as $1-$ dimensional, 2-dimensional, or higher-dimensional arrays. The difference between arrays and tensors (a vector and matrix are special forms of a tensor) is, however, that the mathematical definitions also include rules on how to calculate with these data structures. This book is not a course on mathematics; we are only users of mathematical notations and methods, and mathematical notation help us to keep the text short while being precise. We follow here a common notation of denoting a vector, matrix, or tensor with bold-faced letters, whereas we use regular fonts for scalars. We usually call the input vector a feature vector as the components of this are typically a set feature values of an object. The output could also be a multi-dimensional object such as a vector or tensor itself. Mathematically, we can denote the relations between the input and the output as a function
$$
y=f(\mathbf{x}) .
$$
We consider the function above as a description of the true underlying world, and our task in science or engineering is to find this relation. In the above formula we considered a single output value and several input values for illustration purposes, although we see later that we can extend this readily to multiple output values.
Before proceeding, it is useful to clarify our use of the term “feature.” Features represent components that describe the inputs to our learning systems. Feature values are often measured data in machine learning. Sometime the word “attributes” is used instead. In the most part, we use these terms interchangeably. However, sometimes researchers make a small distinction betwen the terms, using attributes to denote unique content while using feature as a derived value, such as the square of an attribute. This strict distinction is usually not crucial for the understanding of the context so our use of the term feature includes attributes.
Returning to the world model in equation $1.1$, the challenge for machine learning is to find this function, or at least to approximate it sufficiently. Machine learning offers several approaches to deal with this. One approach that we will predominantly follow is to define a general parameterized function
$$
\hat{y}=\hat{f}(\mathbf{x} ; \mathbf{w})
$$
cs代写|机器学习代写machine learning代考|Non-linear regression in high-dimensions
The simplest example of supervised machine learning is linear regression. In linear regression we assume a linear model such as the function,
$$
y=w_{0}+w_{1} x
$$
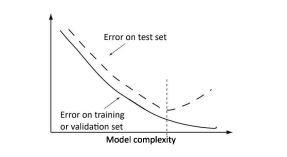
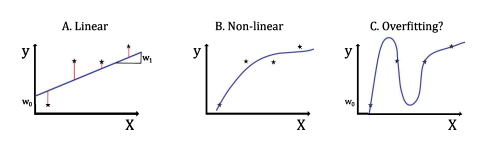
This is a low-dimensional example with only a single feature, value $x$, and a scalar label, value y. Most of us learned in high school to use mean square regression. In this method we choose as values for the offset parameter $w_{0}$ and the slope parameter $w_{1}$ the values that minimize the summed squared difference between the regressed and the data points. This is illustrated in Fig. 1.4A. We will later explain this procedure in more detail. This is an example where data are used to determine the parameters of a parameterized model, and this model with the fitted parameters can then be used to predict $y$ values for new $x$ values. This is in essence supervised learning.What makes modern machine learning go beyond this type of modeling is that we are now usually describing data in high dimensions (many features) and to use non-linear functions. This seems straight forward, but there are several problems in practice going down this route. For example, Fig. 1.4B shows a non-linear function that seems somewhat to describe the pattern of the data much better than the linear model in Fig. 1.4A. However, the non-linear model shown in Fig. 1.4C is also a solution. It even goes through all the training points. This is a particularly difficult problem. If we are allowed to increase the model complexity arbitrarily, then we can always find a model which goes through all the data points. However, the data points might have a simple relation, such as the linear one of Fig. 1.4A, and the variation only represents noise. Fitting the data point with this noise as in Fig. 1.4C does therefore mean that we are overfitting the data.
机器学习代写
cs代写|机器学习代写machine learning代考|Introduction
本章提供了机器学习的高级概述,特别是它与从数据构建模型的关系。我们从历史背景中的一个基本概念开始,并在一个简单的数学术语中将学习问题表述为函数逼近以及概率背景。与更传统的模型相比,我们可以将机器学习描述为高维空间中的非线性回归。本章旨在指出深度学习和贝叶斯网络等不同的子领域如何适应事物的方案,并旨在通过一些近期进展的例子来激发进一步的研究。
机器学习实际上是关于构建机器,通常在软件中,可以学习执行特定任务。机器学习的常见任务示例是从数字图片中识别物体,或者从各种传感器测量中预测机器人或自动驾驶汽车的位置。这些技术在很大程度上促成了通常与人工智能 (AI) 相关的新一波技术。本书致力于介绍该学科的基础知识。
机器学习最近的重要性及其在新工业应用中的快速发展令人叹为观止,预计将发生的众多发展超出了本书的范围。然而,机器学习背后的基本思想知识(其中许多已经存在了一段时间)以及它们用于构建概率模型来描述数据的形式化现在是重要的基本技能。机器学习是关于建模数据。描述数据和不确定性一直是贝叶斯统计和概率论的传统领域。相比之下,许多令人兴奋的最新技术似乎来自现在称为深度学习的领域。本书的具体贡献在于它试图突出这些领域之间的关系。
我们经常简单地说我们从数据中学习,但意识到数据可能意味着几件事是很有用的。在其最基本的形式中,数据通常包括测量值,例如数码相机中的光强度、脑电图 (EEG) 中的电位测量值或股票市场数据的记录。但是,我们学习需要的是一位老师,他可以为我们提供有关这些数据应该预测什么的信息。这样的信息可以采取许多不同的形式。例如,我们可能有一种称为标签的数据形式,例如数码照片中对象的身份。这正是我们学习光学物体识别所需要的信息。教师提供学生(学习者)应该学习预测新输入的期望答案的示例。
cs代写|机器学习代写machine learning代考|Mathematical formulation of the basic learning problem
目前与机器学习成功最相关的大部分是监督学习,有时也称为预测学习。监督学习的基本任务是收集输入数据X,例如图像的像素值、测量的医疗数据或机器人传感器数据,以及预测输出值是例如图像中对象的名称、患者的健康状况或障碍物的位置。通常每个输入都有许多分量,例如图像中的数百万像素值,将这些值收集到数学结构中很有用,例如向量(一维)、矩阵(二维) ,或将这种结构推广到更高维度的张量。我们经常将机器学习问题称为高维问题,在这种情况下,它指的是输入结构中的大量组件,而不是输入张量的维度。
我们主要使用数学术语向量、矩阵和张量来表示数据结构。在编程上下文中,这些通常被描述为1−维、二维或更高维数组。然而,数组和张量(向量和矩阵是张量的特殊形式)之间的区别在于,数学定义还包括如何使用这些数据结构进行计算的规则。这本书不是关于数学的课程;我们只是数学符号和方法的使用者,数学符号帮助我们保持文本简短而精确。我们在这里遵循用粗体字母表示向量、矩阵或张量的通用符号,而我们使用常规字体表示标量。我们通常将输入向量称为特征向量,因为它的组成部分通常是对象的一组特征值。输出也可以是多维对象,例如向量或张量本身。数学上,
是=F(X).
我们将上述函数视为对真实底层世界的描述,而我们在科学或工程中的任务就是找到这种关系。在上面的公式中,出于说明目的,我们考虑了单个输出值和多个输入值,尽管我们稍后会看到我们可以很容易地将其扩展到多个输出值。
在继续之前,澄清我们对术语“特征”的使用是有用的。特征表示描述我们学习系统的输入的组件。特征值通常是机器学习中的测量数据。有时会使用“属性”一词。在大多数情况下,我们可以互换使用这些术语。然而,有时研究人员会在术语之间做出细微的区分,使用属性来表示独特的内容,同时使用特征作为派生值,例如属性的平方。这种严格的区别通常对于理解上下文并不重要,因此我们对术语特征的使用包括属性。
回归方程中的世界模型1.1,机器学习的挑战是找到这个函数,或者至少要充分逼近它。机器学习提供了几种方法来解决这个问题。我们将主要遵循的一种方法是定义一个通用参数化函数
是^=F^(X;在)
cs代写|机器学习代写machine learning代考|Non-linear regression in high-dimensions
监督机器学习最简单的例子是线性回归。在线性回归中,我们假设一个线性模型,例如函数,
是=在0+在1X
这是一个低维示例,只有一个特征,值X,和一个标量标签,值 y。我们大多数人在高中时就学会了使用均方回归。在这种方法中,我们选择偏移参数的值在0和斜率参数在1最小化回归点和数据点之间的平方和差的值。如图 1.4A 所示。我们稍后将更详细地解释此过程。这是一个示例,其中数据用于确定参数化模型的参数,然后可以使用具有拟合参数的模型来预测是新的价值观X价值观。这本质上是监督学习。现代机器学习超越这种建模的原因是我们现在通常描述高维(许多特征)的数据并使用非线性函数。这似乎是直截了当的,但在实践中沿着这条路线走会有几个问题。例如,图 1.4B 显示了一个非线性函数,它似乎比图 1.4A 中的线性模型更好地描述了数据的模式。然而,图 1.4C 所示的非线性模型也是一种解决方案。它甚至通过了所有的训练点。这是一个特别困难的问题。如果允许我们任意增加模型复杂度,那么我们总能找到一个遍历所有数据点的模型。但是,数据点可能具有简单的关系,例如图 1.4A 的线性关系,并且变化仅代表噪声。因此,如图 1.4C 所示,用这种噪声拟合数据点确实意味着我们过度拟合了数据。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
