如果你也在 怎样代写博弈论Game Theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
博弈论是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
statistics-lab™ 为您的留学生涯保驾护航 在代写博弈论Game Theory方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写博弈论Game Theory代写方面经验极为丰富,各种代写博弈论Game Theory相关的作业也就用不着说。
我们提供的博弈论Game Theory及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
经济代写|博弈论代写Game Theory代考|ORDINAL UTILITIES
In this scenario, there are four possible outcomes: Scarlett leaves with vanilla ice cream, which we will label $V$, leaves with chocolate ice cream, labeled $C$, leaves with strawberry ice cream, labeled $S$, or leaves with no ice cream, labeled $N$. Our outcome set is then ${V, C, S, N}$. The rules dictate that Scarlett may choose any outcome that is available.
To model Scarlett’s preferences and build a utility function, we consider the choices she would make when certain outcomes are available. Supposing that all potential outcomes are available, Scarlett would choose $V$; if $C$ were not an available outcome, Scarlett would choose $S$; if only $V$ and $N$ were available outcomes, Scarlett would flip a coin to determine whether to select $V$ or $N$; and if only $C$ and $S$ were available outcomes, Scarlett would be unable to make a choice. While this behavior would be possible, most would find it bizarre: Scarlett’s choice of $V$ when presented with the outcome set ${V, C, S, N}$ suggests she prefers $V$ to $S$, but Scarlett’s choice of $S$ when presented the outcome subset ${V, S, N}$ suggests she prefers $S$ to $V$. To avoid such absurd possibilities, we will assume that individual behavior is governed by self-consistent internal preferences over the outcomes, which is reflected in the mathematical definition of ordinal preferences below.
Definition 2.1.1. A player $i$ is said to have ordinal preferences among outcomes if there exists a utility function $u_i$ from the set $O$ of outcomes into the real numbers, $\mathbb{R}$, such that whenever presented with a subset $O^{\prime} \subseteq O$ of outcomes, player $i$ chooses any of the outcomes that maximize $u_i$ over all outcomes $o \in O^{\prime}$.
To ensure that ordinal preferences align with the players real-world choice behavior, we note that whenever player $i$ prefers outcome $o_j$ over outcome $o_k$, we should have $u_i\left(o_j\right)>$ $u_i\left(o_k\right)$, and when player $i$ is indifferent between $o_j$ and $o_k$ we should have $u_i\left(o_j\right)=u_i\left(o_k\right)$. We now ask under what conditions Scarlett’s outcome choice behavior can be modeled by ordinal preferences and describe three reasonable properties for a self-consistent set of choices. Since it is usually easier for a player to choose between two rather than among many outcomes, these properties will focus on pairwise choices.
First, we want Scarlett’s pairwise choices to be complete, meaning that whenever she is presented with a pair of outcomes, Scarlett is able to make a choice. Equivalently, for each pair of outcomes, $A$ and $B$, exactly one of the following conditions holds: (a) Scarlett chooses $A$ over $B$, (b) Scarlett chooses $B$ over $A$, or (c) Scarlett is willing to flip a coin to determine which outcome to choose (in this case we will often say Scarlett chooses either $A$ or $B$ ). Hence, this condition excludes the following option as a possibility: (d) Scarlett chooses neither $A$ nor $B$. (When we want the rules to allow a player to choose none of the options, we must include that as an outcome, as we did in the Ice Cream Parlor scenario.) For (a), we will assign utilities so that $u(A)>u(B)$. Likewise for (b) we will assign utilities so that $u(B)>u(A)$. Finally for (c), since Scarlett is willing to flip a coin to determine the outcome, we assume she is indifferent between $A$ and $B$ and assign $u(A)=u(B)$.
经济代写|博弈论代写Game Theory代考|VON NEUMANN-MORGENSTERN UTILITIES
A significant limitation of ordinal preferences and their associated utility functions is that they cannot describe the intensity of a player’s preference for a particular outcome. That is, they cannot capture the difference between Scarlett preferring vanilla ice cream over chocolate ice cream and Scarlett so strongly preferring vanilla that she would pay for it rather than have a free serving of chocolate. Notice how we have once again translated our intuitive sense of internal preference intensity into something that is observable (a real-world choice) so we can create a utility function based on these choices. While asking players to choose among outcomes that include the receipt or payment of money would be one observable way to determine intensity of preferences, we will take an approach that does not rely on the availability of money.
We begin by introducing a new, probability-based outcome called a lottery. Suppose that when a second customer, Regis, enters the ice cream parlor, he encounters a college student conducting a taste test involving different flavors of ice cream. The college student offers Regis the choice of either a sample of chocolate ice cream (his second-most favorite) or an unknown sample that is either vanilla (his favorite) or strawberry (his least favorite). The second option in this example is a simple lottery.
Definition 2.2.1. Given a set of outcomes, $O$, a simple lottery is a probability distribution over this set. When $O=\left{o_1, o_2, \ldots, o_m\right}$, a finite set, a simple lottery can be denoted by $p_1 o_1+p_2 o_2+\ldots+p_m o_m$ where $p_i$ is the probability of outcome $o_i$. A compound lottery is a probability distribution over other lotteries. Because an outcome $o \in O$ can be written as the simple lottery $1 o$, we see that $O \subset \mathcal{L}$, the set of all (simple and compound) lotteries.
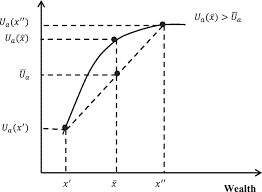
Tó reveál thè strength of a player’s préference for one outcomé over another, wè must examine not nnly chnires hetween single nutromes hut chnices hetween single nutcomes and lotteries. Suppose Regis prefers vanilla $V$ over chocolate $C$ and prefers $C$ over strawberry $S$. The choice Regis makes between $C$ and the lottery $0.5 S+0.5 V$ tells us about the strength of his preference for $V$ over $C$ and for $C$ over $S$. If he would choose either of the two possibilities, then the strength of Regis’s preference for $C$ is exactly halfway between $S$ and $V$. If Regis were to choose $C$ over $0.5 S+0.5 \mathrm{~V}$, it reveals that his preference intensity for $C$ is closer to $V$ than to $S$. If Regis were willing to choose either $C$ or the lottery $0.1 S+0.9 \mathrm{~V}$, it would reveal that his preference for $V$ over $C$ is very small and his preference for $C$ over $S$ is relatively large. However, if he were instead willing to choose $C$ or the lottery $0.9 S+0.1 \mathrm{~V}$, it would reveal a strong preference for $V$ over $C$ and that his preferences for $C$ over $S$ is small. When a player is willing to choose either of two lotteries, this reveals the player is indifferent between these choices. This motivates the following generalization of the utility function concept.
博弈论代考
经济代写|博弈论代写Game Theory代考|ORDINAL UTILITIES
在这种情况下,有四种可能的结果: Scarlett 带着香草冰淇淋离开,我们将其标记为 $V$ ,带有巧克力冰 淇淋的叶子,贴有标签 $C$ ,叶子和草莓冰淇淋,贴有标签 $S$ ,或没有冰淇淋的叶子,贴有标签 $N$. 我们的 结果集是 $V, C, S, N$. 规则规定斯嘉丽可以选择任何可用的结果。
为了对 Scarlett 的偏好进行建模并构建效用函数,我们考虑了当某些结果可用时她会做出的选择。假设 所有可能的结果都是可用的,斯嘉丽会选择 $V$; 如果 $C$ 没有可用的结果,斯嘉丽会选择 $S$; 要是 $V$ 和 $N$ 如果 有可用的结果,斯嘉丽会掷硬币来决定是否选择 $V$ 要么 $N$; 如果只有 $C$ 和 $S$ 如果有可用的结果,斯嘉丽将 无法做出选择。虽然这种行为是可能的,但大多数人会觉得很奇怪:斯嘉丽选择 $V$ 当出现结果集时 $V, C, S, N$ 表明她更喜欢 $V$ 到 $S$, 但思嘉的选择 $S$ 当呈现结果子集时 $V, S, N$ 表明她更喜欢 $S$ 到 $V$. 为了避 免这种荒谬的可能性,我们将假设个人行为受对结果的自洽内部偏好的支配,这反映在下面的序数偏好 的数学定义中。
定义 2.1.1。一个玩家 $i$ 如果存在效用函数,则据说在结果之间具有顺序偏好 $u_i$ 从集合 $O$ 结果转化为实 数, $\mathbb{R}$ ,这样每当出现一个子集 $O^{\prime} \subseteq O$ 结果,玩家 $i$ 选择任何最大化的结果 $u_i$ 在所有结果上 $o \in O^{\prime}$.
为了确保序数偏好与玩家在现实世界中的选择行为一致,我们注意到每当玩家 $i$ 更喜欢结果 $o_j$ 超过结果 $o_k$ ,我们本应该 $u_i\left(o_j\right)>u_i\left(o_k\right)$ ,当玩家 $i$ 无所谓 $o_j$ 和 $o_k$ 我们本应该 $u_i\left(o_j\right)=u_i\left(o_k\right)$. 我们现在询问 在什么条件下 Scarlett 的结果选择行为可以通过序数偏好来建模,并描述自洽选择集的三个合理属性。 由于玩家通常更容易在两个结果之间做出选择,而不是在许多结果中做出选择,因此这些属性将侧重于 成对选择。
首先,我们㳍望 Scarlett 的成对选择是完整的,这意味着无论何时向她呈现一对结果,Scarlett 都能够做 出选择。等价地,对于每对结果, $A$ 和 $B$, 怙好满足以下条件之一:(a) Scarlett 选择 $A$ 超过 $B$ , (b) 思嘉选 择 $B$ 超过 $A$ ,或者 (c) Scarlett 愿意郑硬币来决定选择哪个结果(在这种情况下,我们通常会说 Scarlett 选择 $A$ 要么 $B$ ). 因此,这个条件排除了以下选项的可能性: (d) Scarlett 既不选择 $A$ 也不 $B$. (当我们㣇望 规则允许玩家不选择任何选项时,我们必须将其作为结果包括在内,就像我们在冰淇淋店场景中所做的 那样。)对于 (a),我们将分配实用程序,以便 $u(A)>u(B)$. 同样对于 (b) 我们将分配实用程序,以便 $u(B)>u(A)$. 最后对于 (c),由于 Scarlett 愿意掷硬币来决定结果,我们假设她对两者无动于衷 $A$ 和 $B$ 并分配 $u(A)=u(B)$.
经济代写|博弈论代写Game Theory代考|VON NEUMANN-MORGENSTERN UTILITIES
序数偏好及其相关效用函数的一个重要限制是它们无法描述玩家对特定结果的偏好强度。也就是说,他 们无法区分 Scarlett 更喜欢香草冰淇淋而不是巧克力冰淇淋,以及 Scarlett 如此强烈地喜欢香草以至于 她愿意为它付钱而不是免费享用巧克力之间的区别。请注意我们如何再次将我们对内部偏好强度的直觉 转化为可观察的东西 (现实世界的选择),因此我们可以根据这些选择创建效用函数。虽然要求玩家在 包括收款或付款在内的结果中进行选择是确定偏好强度的一种可观察方法,但我们将采用一种不依赖于 金钱可用性的方法。
我们首先介绍一种新的、基于概率的结果,称为彩票。假设当第二位顾客 Regis 进入冰淇淋店时,他遇 到一名大学生正在对不同口味的冰淇淋进行味觉测试。这位大学生让瑞吉斯选择巧克力冰淇淋样品(他 第二喜欢) 或末知样品,香草 (他最喜欢) 或草莓(他最不喜欢) 。此示例中的第二个选项是简单的彩 票。
定义 2.2.1。给定一组结果, $O$ ,一个简单的彩票是这个集合的概率分布。什么时候
O=\left{0_1,o_2, Vdots, o_m\right } } \text { ,一个有限集,一个简单的彩票可以表示为 }
$p_1 o_1+p_2 o_2+\ldots+p_m o_m$ 在哪里 $p_i$ 是结果的概率 $o_i$. 复合彩票是其他彩票的概率分布。因为一个结 果 $o \in O$ 可以写成简单的彩票 $l o$ ,我们看到 $O \subset \mathcal{L}$ ,所有(简单和复合) 彩票的集合。
为了揭示玩家对一个结果的偏好程度优于另一个结果,我们不仅要检查单个结果之间的关系,还要检查 单个结果和彩票之间的关系。假设 Regis 更喜欢香草味 $V$ 巧克力 $C$ 并且喜欢 $C$ 在草莓上 $S$. 瑞吉斯的选择 $C$ 和彩票 $0.5 S+0.5 V$ 告诉我们他偏爱的强度 $V$ 超过 $C$ 并为 $C$ 超过 $S$. 如果他选择这两种可能性中的任何 一种,那么 Regis 偏好的强度 $C$ 恰好在中间 $S$ 和 $V$. 如果瑞吉斯选择 $C$ 超过 $0.5 S+0.5 \mathrm{~V}$ ,它揭示了他对 $C$ 更接近 $V$ 比到 $S$. 如果瑞吉斯愿意选择 $C$ 或彩票 $0.1 S+0.9 \mathrm{~V}$ ,这将揭示他对 $V$ 超过 $C$ 很小,他偏爱 $C$ 超过 $S$ 比较大。但是,如果他愿意选择 $C$ 或彩票 $0.9 S+0.1 \mathrm{~V}$ ,它会显示出对 $V$ 超过 $C$ 他的偏好 $C$ 超过 $S$ 是小。当玩家愿意选择两个彩票中的任何一个时,这表明玩家对这些选择无动于衷。这激发了效用函数概念的以下概括。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
