数学代写|图论作业代写Graph Theory代考|MTH607
如果你也在 怎样代写图论Graph Theory 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。图论Graph Theory有趣的部分原因在于,图可以用来对某些问题中的情况进行建模。这些问题可以在图表的帮助下进行研究(并可能得到解决)。因此,图形模型在本书中经常出现。然而,图论是数学的一个领域,因此涉及数学思想的研究-概念和它们之间的联系。我们选择包含的主题和结果是因为我们认为它们有趣、重要和/或代表主题。
图论Graph Theory通过熟悉许多过去和现在对图论的发展负责的人,可以增强对图论的欣赏。因此,我们收录了一些关于“图论人士”的有趣评论。因为我们相信这些人是图论故事的一部分,所以我们在文中讨论了他们,而不仅仅是作为脚注。我们常常没有认识到数学是一门有生命的学科。图论是人类创造的,是一门仍在不断发展的学科。
statistics-lab™ 为您的留学生涯保驾护航 在代写图论Graph Theory方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写图论Graph Theory代写方面经验极为丰富,各种代写图论Graph Theory相关的作业也就用不着说。
数学代写|图论作业代写Graph Theory代考|Ramsey properties and connectivity
According to Ramsey’s theorem, every large enough graph $G$ has a very dense or a very sparse induced subgraph of given order, a $K^r$ or $\overline{K^r}$. If we assume that $G$ is connected, we can say a little more:
Proposition 9.4.1. For every $r \in \mathbb{N}$ there is an $n \in \mathbb{N}$ such that every connected graph of order at least $n$ contains $K^r, K_{1, r}$ or $P^r$ as an induced subgraph.
Proof. Let $d+1$ be the Ramsey number of $r$, let $n:=\frac{d}{d-2}(d-1)^r$, and let $G$ be a graph of order at least $n$. If $G$ has a vertex $v$ of degree at least $d+1$ then, by Theorem 9.1.1 and the choice of $d$, either $N(v)$ induces a $K^r$ in $G$ or ${v} \cup N(v)$ induces a $K_{1, r}$. On the other hand, if $\Delta(G) \leqslant d$, then by Proposition 1.3.3 $G$ has radius $>r$, and hence contains two vertices at a distance $\geqslant r$. Any shortest path in $G$ between these two vertices contains a $P^r$.
In principle, we could now look for a similar set of ‘unavoidable’ $k$-connected subgraphs for any given connectivity $k$. To keep thse ‘unavoidable sets’ small, it helps to relax the containment relation from ‘induced subgraph’ for $k=1$ (as above) to ‘topological minor’ for $k=2$, and on to ‘minor’ for $k=3$ and $k=4$. For larger $k$, no similar results are known.
Proposition 9.4.2. For every $r \in \mathbb{N}$ there is an $n \in \mathbb{N}$ such that every 2-connected graph of order at least $n$ contains $C^r$ or $K_{2, r}$ as a topological minor.
Proof. Let $d$ be the $n$ associated with $r$ in Proposition 9.4.1, and let $G$ be a 2-connected graph with at least $\frac{d}{d-2}(d-1)^r$ vertices. By Proposition 1.3.3, either $G$ has a vertex of degree $>d$ or $\operatorname{diam} G \geqslant \operatorname{rad} G>r$.
In the latter case let $a, b \in G$ be two vertices at distance $>r$. By Menger’s theorem (3.3.6), $G$ contains two independent $a-b$ paths. These form a cycle of length $>r$.
数学代写|图论作业代写Graph Theory代考|Simple sufficient conditions
What kind of condition might be sufficient for the existence of a Hamilton cycle in a graph $G$ ? Purely global assumptions, like high edge density, will not be enough: we cannot do without the local property that every vertex has at least two neighbours. But neither is any large (but constant) minimum degree sufficient: it is easy to find graphs without a Hamilton cycle whose minimum degree exceeds any given constant bound.
The following classic result derives its significance from this background:
Theorem 10.1.1. (Dirac 1952)
Every graph with $n \geqslant 3$ vertices and minimum degree at least $n / 2$ has a Hamilton cycle.
Proof. Let $G=(V, E)$ be a graph with $|G|=n \geqslant 3$ and $\delta(G) \geqslant n / 2$. Then $G$ is connected: otherwise, the degree of any vertex in the smallest component $C$ of $G$ would be less than $|C| \leqslant n / 2$.
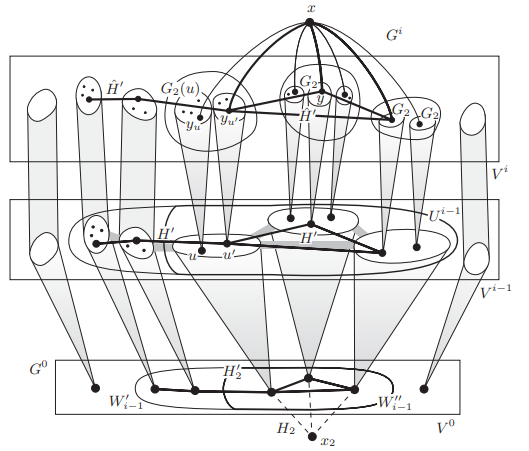
Let $P=x_0 \ldots x_k$ be a longest path in $G$. By the maximality of $P$, all the neighbours of $x_0$ and all the neighbours of $x_k$ lie on $P$. Hence at least $n / 2$ of the vertices $x_0, \ldots, x_{k-1}$ are adjacent to $x_k$, and at least $n / 2$ of these same $k<n$ vertices $x_i$ are such that $x_0 x_{i+1} \in E$. By the pigeon hole principle, there is a vertex $x_i$ that has both properties, so we have $x_0 x_{i+1} \in E$ and $x_i x_k \in E$ for some $i<k$ (Fig. 10.1.1).
We claim that the cycle $C:=x_0 x_{i+1} P x_k x_i P x_0$ is a Hamilton cycle of $G$. Indeed, since $G$ is connected, $C$ would otherwise have a neighbour in $G-C$, which could be combined with a spanning path of $C$ into a path longer than $P$.
图论代考
数学代写|图论作业代写Graph Theory代考|Ramsey properties and connectivity
根据拉姆齐定理,每个足够大的图$G$都有一个非常密集或非常稀疏的给定阶的诱导子图$K^r$或$\overline{K^r}$。如果我们假设$G$是连接的,我们可以多说一点:
提案9.4.1对于每个$r \in \mathbb{N}$,都存在一个$n \in \mathbb{N}$,使得每个至少为$n$阶的连通图都包含$K^r, K_{1, r}$或$P^r$作为诱导子图。
证明。设$d+1$为$r$的拉姆齐数,设$n:=\frac{d}{d-2}(d-1)^r$,设$G$为至少为$n$的有序图。如果$G$有一个顶点$v$的度数至少为$d+1$,那么根据定理9.1.1和$d$的选择,要么$N(v)$在$G$中衍生出一个$K^r$,要么${v} \cup N(v)$衍生出一个$K_{1, r}$。另一方面,如果$\Delta(G) \leqslant d$,则根据命题1.3.3 $G$的半径为$>r$,因此包含两个距离为$\geqslant r$的顶点。在$G$中这两个顶点之间的任何最短路径都包含$P^r$。
原则上,对于任何给定的连通性$k$,我们现在可以寻找类似的一组“不可避免的”$k$连接子图。为了保持这些“不可避免的集合”较小,它有助于将包含关系从$k=1$的“诱导子图”(如上所述)放宽到$k=2$的“拓扑次要”,然后再放宽到$k=3$和$k=4$的“次要”。对于更大的$k$,没有类似的结果。
提案9.4.2。对于每个$r \in \mathbb{N}$,都存在一个$n \in \mathbb{N}$,使得每个至少为$n$阶的2连通图都包含$C^r$或$K_{2, r}$作为拓扑次元。
证明。设$d$为命题9.4.1中与$r$相关联的$n$,设$G$为至少有$\frac{d}{d-2}(d-1)^r$个顶点的2连通图。根据命题1.3.3,$G$有一个度数为$>d$或$\operatorname{diam} G \geqslant \operatorname{rad} G>r$的顶点。
在后一种情况下,设$a, b \in G$为距离为$>r$的两个顶点。根据门格尔定理(3.3.6),$G$包含两个独立的$a-b$路径。这些形成了一个长度为$>r$的循环。
数学代写|图论作业代写Graph Theory代考|Simple sufficient conditions
什么样的条件可能是图中存在汉密尔顿环的充分条件$G$ ?纯粹的全局假设,比如高边缘密度,是不够的:我们不能没有每个顶点至少有两个邻居的局部性质。但是,任何大的(但恒定的)最小度都是不够的:很容易找到没有Hamilton循环的图,其最小度超过任何给定的常数界。
下面这个经典结论的意义就来源于这个背景:
定理10.1.1。(狄拉克1952)
每个顶点为$n \geqslant 3$且最小度至少为$n / 2$的图都有一个Hamilton循环。
证明。设$G=(V, E)$为具有$|G|=n \geqslant 3$和$\delta(G) \geqslant n / 2$的图形。那么$G$是连通的,否则$G$的最小分量$C$中任意顶点的度数都小于$|C| \leqslant n / 2$。
设$P=x_0 \ldots x_k$为$G$的最长路径。根据$P$的最大值,$x_0$的所有邻居和$x_k$的所有邻居都在$P$上。因此,至少$n / 2$个顶点$x_0, \ldots, x_{k-1}$与$x_k$相邻,并且至少$n / 2$个相同的$k<n$个顶点$x_i$与$x_0 x_{i+1} \in E$相邻。根据鸽子洞原理,有一个顶点$x_i$同时具有这两个属性,因此对于某些$i<k$,我们有$x_0 x_{i+1} \in E$和$x_i x_k \in E$(图10.1.1)。
我们声称周期$C:=x_0 x_{i+1} P x_k x_i P x_0$是一个$G$的汉密尔顿周期。事实上,因为$G$是连通的,否则$C$在$G-C$中就会有一个邻居,它可以与$C$的生成路径组合成一条比$P$长的路径。

统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。