如果你也在 怎样代写图论Graph Theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
在数学中,图论是对图的研究,它是用来模拟对象之间成对关系的数学结构。这里,图由顶点(也称为节点或点)组成,这些顶点由边(也称为链接或线)连接。
statistics-lab™ 为您的留学生涯保驾护航 在代写图论Graph Theory方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写图论Graph Theory代写方面经验极为丰富,各种代写图论Graph Theory相关的作业也就用不着说。
我们提供的图论Graph Theory及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
数学代写|图论作业代写Graph Theory代考|TRIVIAL FOUR-COLORING
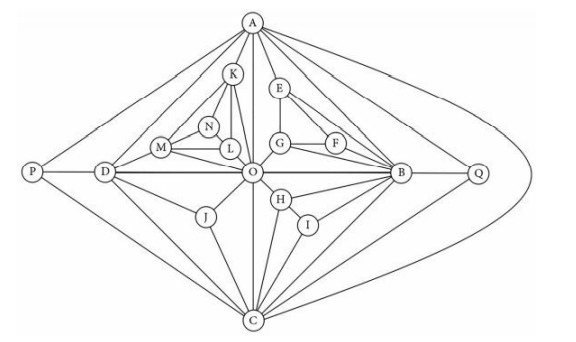
A vertex with a degree equal to three is connected to exactly three other vertices. A vertex with degree three is guaranteed to be four-colorable. Why? Regardless of which colors the other three vertices have, there will always be at least one color remaining that is different from the colors of those three vertices. For example, consider the diagram below, which is “zoomed in” on a vertex with degree three. The rest of the graph is irrelevant to the current discussion. Just focus on the vertex with degree three and the three vertices to which it is connected. If $\mathrm{A}$ is red, B is blue, and $\mathrm{C}$ is green, for example, then $\mathrm{D}$ can be yellow. If instead $\mathrm{A}$ is yellow, $\mathrm{B}$ is green, and $C$ is yellow, then $\mathrm{D}$ can be red or blue. No matter which colors you choose for $A, B$, and $C$, there will always be at least one color left over for D. Any vertex with degree three (or less) may be removed from a graph, provided that we also remove the edges connecting it to the other vertices. If a graph is four-colorable after the vertices with degree three have been removed, it will still be four-colorable when the vertices with degree three are replaced. The examples of this chapter will illustrate this concept, including cases where vertices that originally had higher degrees may also be removed.
This means that we don’t need to worry about any graphs that have at least one vertex with degree three. If we can prove the four-color theorem for all planar graphs that only have vertices with degree four and higher, it will follow that all planar graphs are four-colorable.
For example, the MPG on the left has three vertices with degree three: D, F, and I. When we remove these vertices and their connecting edges, we obtain the middle MPG. Although vertices $C, G$, and $J$ had previously been degree four, after the edges connecting $\mathrm{D}, \mathrm{F}$, and I were removed, $\mathrm{C}, \mathrm{G}$, and $\mathrm{J}$ became degree three. We may now remove vertices $C, G$, and $J$. When we do this, even the remaining vertices (A, B, E, and $\mathrm{H}$ ) are now degree three. Since the entire graph has unraveled through the process of removing vertices of degree three and their connecting edges, this graph is one of many graphs that are trivially four-colorable.
There are a great many MPG’s with at least one vertex with degree three which completely unravel (and thus are trivially four-colorable) when vertices of degree three are removed from the graph. However, this is not always the case, as the next example shows.
The MPG on the left has one vertex with degree three: F. In this case, when F and its connecting edges are removed, the new MPG doesn’t have any vertices with a degree less than four. In this example, only one vertex can be removed. Once the MPG on the right is shown to be four-colorable, it will follow that the MPG on the left is also four-colorable.
数学代写|图论作业代写Graph Theory代考|SEPARATING TRIANGLES
Imagine making a MPG with a $\mathrm{K}{4}$ subgraph where every vertex of the $\mathrm{K}{4}$ has a degree of four or higher. Start by thinking about the $\mathrm{K}_{4}$ shown below. In order for vertex $D$ to have a degree of four or higher, we must add new vertices inside at least one of the faces.Note that $\mathrm{K}{4}$ has four faces: $\mathrm{ABD}, \mathrm{ACD}, \mathrm{BCD}$, and the outside face $\mathrm{ABC}$ corresponding to the infinite area outside. If we add new vertices in at least two of these faces (well, for $\mathrm{ABC}$ it would be “out” rather than “in”), we can make a MPG where all of the vertices of the $K{4}$ subgraph have a degree of at least four. An example is shown below.
Find $\mathrm{A}, \mathrm{B}, \mathrm{C}$, and $\mathrm{D}$ in the triangle above. This was our original $\mathrm{K}{4}$, which is now a subgraph of a MPG with 10 vertices. We added vertices $E, F$, and $G$ in face $\mathrm{ABD}$, and added vertices $\mathrm{H}$, I, and $\mathrm{J}$ “in” the outside face $\mathrm{ABC}$ (when a face corresponds to the infinite area outside, the area of the face is “out” of the face rather than “in” it). We then added enough edges to triangulate the graph, turning it into a MPG. For $\mathrm{V}=10$ vertices, we need a total of $E=3 V-6=3(10)-6=24$ edges (arranged so that every face has three edges). The way we chose to add the needed edges, note that all 10 vertices of the MPG have a degree of at least four, including all four vertices of the original $\mathrm{K}{4}$ subgraph.
Every $\mathrm{K}_{4}$ subgraph has a separating triangle. What does this mean? A separating triangle, which we will abbreviate ST, is a triangle consisting of three vertices and three edges, where the triangle isn’t one of the faces. A ST has at least two faces inside of it and at least two faces outside of it. (Note that one of the faces outside of a ST can be the infinite area outside of the MPG.)
In the previous example, ABD is a ST because ABD isn’t a face and because there are at least two faces inside and at least two faces outside of ABD. We call it a ST because vertices A, B, and D divide the MPG into two smaller MPG’s, as seen in the diagram below. Observe that triangle ABD appears in both MPG’s below, and now ABD is a face (whereas it wasn’t in the original graph). Any MPG that has a ST can similarly be split into two separate MPG’s. (There is actually a second ST in the MPG below and on the previous page: triangle $\mathrm{ABC}$.)
数学代写|图论作业代写Graph Theory代考|HAMILTONIAN CYCLES
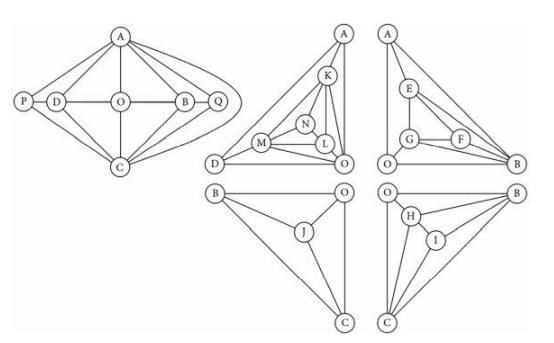
A circuit refers to a path in a graph that begins and ends at the same vertex (meaning that the path is a closed loop), while a cycle refers to a circuit that doesn’t repeat any vertices. A $H a m i l t o n i a n ~ c y c l e, ~ w h i c h ~ w e ~ w i l l ~ a b b r e v i a t e ~$ $\mathrm{HC}$, is a cycle that involves every vertex in a graph [Ref. 10]. Many (but not all) MPG’s have a HC. If a MPG has a HC, there exists some way to begin at one vertex, travel along an edge to another vertex, travel along another edge to another vertex, continuing to do so until every vertex is visited exactly once, and then travel along one more edge to return to the original vertex. An example of a HC is shown below.
The MPG on the left includes the HC shown on the right. If you start at vertex H, for example, you can then trace the cycle HBGAFEDCLIJKMPNOH. It’s important to finish on the same vertex as you start. (If there isn’t an edge returning to the starting vertex from the ending vertex, then it’s a Hamiltonian “path,” not a “cycle.”) When a HC exists for a MPG, there are often multiple HC’s. For example, we could start out HBAGFE instead of HBGAFE and still obtain a HC. There are numerous HC’s available for the above MPG.
An example of a MPG that doesn’t have a HC is shown on the following page. This graph is known as the Goldner-Harary graph [Ref. 11].
The best we can do with the above MPG is GDHAEIFBKCJ, but although we were able to use all 11 vertices going from $\mathrm{G}$ thru $\mathrm{J}$, unfortunately there isn’t an edge allowing a return from the final point (J) to the initial point (G). What if we don’t start at G? Okay, let’s try it again: CKBFIEAHDG. This time, we didn’t even reach J (we could have after D, but then we wouldn’t have reached G). Another option is JDHAEIGCFBK. We visited all 11 vertices once again, but were unable to return to the starting point (J) from the final point (K). Try as you might, no HC exists for the MPG above. (We did find a Hamiltonian path, but that’s not the same as a Hamiltonian cycle.)
How can you tell whether a MPG will have a HC? It turns out that if a MPG doesn’t have a ST, then it has a HC [Ref. 12]. Recall from Chapter 12 that ST stands for “separating triangle.” (However, if a MPG has ST’s, this doesn’t mean it won’t have a HC; it’s possible for a MPG to have ST’s and still have a HC.)
The previous graph has 4 ST’s: ABI, ADI, BCI, and CDI. Each of these ST’s has 3 faces inside of it and 15 faces outside of it. As far as the four-color theorem is concerned, the ST’s of this particular graph are trivial, since the vertex inside of each ST is degree three. The vertices inside of the ST’s are H, E, F, and G. Recall from Chapter 11 that we may remove any vertices with degree three from the graph along with their connecting edges. When we do this, we obtain the following graph, which now has a HC.
图论代考
数学代写|图论作业代写Graph Theory代考|TRIVIAL FOUR-COLORING
度数等于 3 的顶点恰好连接到其他三个顶点。度数为三的顶点保证是四色的。为什么?无论其他三个顶点具有哪种颜色,总会有至少一种颜色与这三个顶点的颜色不同。例如,考虑下图,它在一个度数为 3 的顶点上“放大”。图的其余部分与当前的讨论无关。只关注度数为 3 的顶点和它所连接的三个顶点。如果一种是红色,B 是蓝色,并且C是绿色的,例如,那么D可以是黄色的。如果相反一种是黄色的,乙是绿色的,并且C是黄色的,那么D可以是红色或蓝色。无论您选择哪种颜色一种,乙, 和C, 总是会为 D 留下至少一种颜色。只要我们还删除了将其连接到其他顶点的边,任何具有三度(或更少)的顶点都可以从图中删除。如果一个图在移除了三阶顶点之后是四色的,那么当三阶顶点被替换时,它仍然是四色的。本章的示例将说明这个概念,包括原本具有较高度数的顶点也可能被删除的情况。
这意味着我们不需要担心任何至少有一个顶点为三度的图。如果我们可以证明所有只有四次或更高阶顶点的平面图的四色定理,那么所有平面图都是四色的。
例如,左边的 MPG 有三个度数为 3 的顶点:D、F 和 I。当我们移除这些顶点及其连接边时,我们得到中间的 MPG。虽然顶点C,G, 和Ĵ以前是四度,在边缘连接之后D,F,我被删除了,C,G, 和Ĵ变成了三级。我们现在可以删除顶点C,G, 和Ĵ. 当我们这样做时,即使是剩余的顶点(A、B、E 和H) 现在是三级。由于整个图已通过删除三度顶点及其连接边的过程解开,因此该图是许多可简单地四色的图之一。
当从图中删除三阶顶点时,有很多 MPG 具有至少一个三阶顶点,它们完全解开(因此很容易变成四色)。但是,情况并非总是如此,如下一个示例所示。
左边的 MPG 有一个度数为 3 的顶点:F。在这种情况下,当 F 及其连接边被移除时,新的 MPG 没有任何度数小于 4 的顶点。在此示例中,只能删除一个顶点。一旦右边的 MPG 显示为四色,那么左边的 MPG 也是四色的。
数学代写|图论作业代写Graph Theory代考|SEPARATING TRIANGLES
想象一下用一个 MPGķ4子图,其中的每个顶点ķ4具有四级或更高的学位。从思考问题开始ķ4如下图所示。为了顶点D要获得 4 或更高的度数,我们必须在至少一个面内添加新顶点。请注意ķ4有四个面孔:一种乙D,一种CD,乙CD, 和外表面一种乙C对应于外面的无限区域。如果我们在其中至少两个面中添加新顶点(好吧,对于一种乙C它会是“out”而不是“in”),我们可以制作一个 MPG,其中所有的顶点ķ4子图的度数至少为四。一个例子如下所示。
寻找一种,乙,C, 和D在上面的三角形中。这是我们原来的ķ4,现在是具有 10 个顶点的 MPG 的子图。我们添加了顶点和,F, 和G面对一种乙D,并添加顶点H, 我和Ĵ“在”外面一种乙C(当一个面对应于外面的无限区域时,面的区域是“外面”而不是“里面”)。然后我们添加了足够多的边来对图进行三角剖分,将其变成 MPG。为了在=10顶点,我们总共需要和=3在−6=3(10)−6=24边(排列成每个面都有三个边)。我们选择添加所需边的方式,注意 MPG 的所有 10 个顶点的度数至少为 4,包括原始的所有四个顶点ķ4子图。
每一个ķ4子图有一个分隔三角形。这是什么意思?我们将缩写为 ST 的分离三角形是由三个顶点和三个边组成的三角形,其中三角形不是其中一个面。ST 在其内部至少有两个面,在其外部至少有两个面。(请注意,ST 之外的面之一可以是 MPG 之外的无限区域。)
在前面的示例中,ABD 是一个 ST,因为 ABD 不是一个面,并且因为 ABD 内部至少有两个面,而 ABD 外部至少有两个面。我们称它为 ST,因为顶点 A、B 和 D 将 MPG 分成两个较小的 MPG,如下图所示。观察三角形 ABD 出现在下面的两个 MPG 中,现在 ABD 是一张脸(而它不在原始图中)。任何具有 ST 的 MPG 都可以类似地分成两个独立的 MPG。(其实MPG下面和上一页还有第二个ST:triangle一种乙C.)
数学代写|图论作业代写Graph Theory代考|HAMILTONIAN CYCLES
回路是指图形中起点和终点在同一顶点的路径(意味着该路径是一个闭环),而循环是指不重复任何顶点的回路。A$ H amiltonian~cycle,~which~we~will~缩写~\mathrm{HC}$, 是一个涉及图中每个顶点的循环 [Ref. 10]。许多(但不是全部)MPG 都有 HC。如果 MPG 具有 HC,则存在某种方式可以从一个顶点开始,沿着一条边到另一个顶点,沿着另一条边到另一个顶点,继续这样做,直到每个顶点都被访问一次,然后沿着一个更多的边返回到原来的顶点。HC 的示例如下所示。
左侧的 MPG 包括右侧所示的 HC。例如,如果从顶点 H 开始,则可以跟踪循环 HBGAFEDCLIJKMPNOH。在开始时在同一个顶点上完成是很重要的。(如果没有一条边从结束顶点返回到起始顶点,那么它是哈密顿“路径”,而不是“循环”。)当 MPG 存在 HC 时,通常有多个 HC。例如,我们可以启动 HBAGFE 而不是 HBGAFE,但仍然获得 HC。有许多 HC 可用于上述 MPG。
下页显示了一个没有 HC 的 MPG 示例。该图被称为 Goldner-Harary 图 [Ref. 11]。
我们可以用上述 MPG 做的最好的事情是 GDHAEIFBKCJ,但是虽然我们能够使用所有 11 个顶点G直通Ĵ,不幸的是,没有一条边允许从终点 (J) 返回到初始点 (G)。如果我们不从 G 开始呢?好的,让我们再试一次:CKBFIEAHDG。这一次,我们甚至没有到达 J(我们可以在 D 之后到达,但我们不会到达 G)。另一种选择是 JDHAEIGCFBK。我们再次访问了所有 11 个顶点,但无法从终点 (K) 返回起点 (J)。尽你所能,上面的 MPG 不存在 HC。(我们确实找到了哈密顿路径,但这与哈密顿循环不同。)
如何判断 MPG 是否有 HC?事实证明,如果 MPG 没有 ST,那么它就有 HC [Ref. 12]。回想一下第 12 章,ST 代表“分离三角形”。(但是,如果 MPG 有 ST,这并不意味着它不会有 HC;MPG 有可能有 ST 并且仍然有 HC。)
上图有 4 个 ST:ABI、ADI、BCI 和 CDI。这些 ST 中的每一个都有 3 个内部面和 15 个外部面。就四色定理而言,这个特定图的 ST 是微不足道的,因为每个 ST 内部的顶点都是三度的。ST 内部的顶点是 H、E、F 和 G。回想一下第 11 章,我们可以从图中删除任何度数为 3 的顶点及其连接边。当我们这样做时,我们得到下图,它现在有一个 HC。

统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
| R语言代写 | 问卷设计与分析代写 |
| PYTHON代写 | 回归分析与线性模型代写 |
| MATLAB代写 | 方差分析与试验设计代写 |
| STATA代写 | 机器学习/统计学习代写 |
| SPSS代写 | 计量经济学代写 |
| EVIEWS代写 | 时间序列分析代写 |
| EXCEL代写 | 深度学习代写 |
| SQL代写 | 各种数据建模与可视化代写 |
AIOSEO設定
切换面板:AIOSEO設定
- 文章
- 区块
6个区块514字打开发布面板
- 文章
The graphs above are incomplete. These figures only show a vertex with degree four (vertex E), its nearest neighbors (A, B, C, and D), and segments of A-C Kempe chains. The entire graphs would also contain several other vertices (especially, more colored the same as B or D) and enough edges to be MPG’s. The left figure has A connected to $C$ in a single section of an A-C Kempe chain (meaning that the vertices of this chain are colored the same as A and C). The left figure shows that this A-C Kempe chain prevents B from connecting to $\mathrm{D}$ with a single section of a B-D Kempe chain. The middle figure has A and C in separate sections of A-C Kempe chains. In this case, B could connect to D with a single section of a B-D Kempe chain. However, since the A and C of the vertex with degree four lie on separate sections, the color of C’s chain can be reversed so that in the vertex with degree four, C is effectively recolored to match A’s color, as shown in the right figure. Similarly, D’s section could be reversed in the left figure so that D is effectively recolored to match B’s color.
Kempe also attempted to demonstrate that vertices with degree five are fourcolorable in his attempt to prove the four-color theorem [Ref. 2], but his argument for vertices with degree five was shown by Heawood in 1890 to be insufficient [Ref. 3]. Let’s explore what happens if we attempt to apply our reasoning for vertices with degree four to a vertex with degree five.
数学代写|图论作业代写Graph Theory代考|The previous diagrams
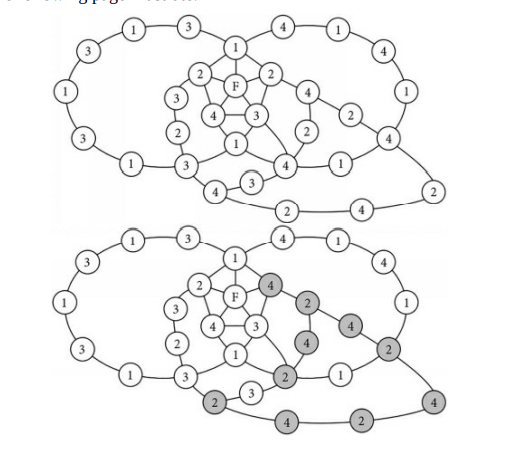
The previous diagrams show that when the two color reversals are performed one at a time in the crossed-chain graph, the first color reversal may break the other chain, allowing the second color reversal to affect the colors of one of F’s neighbors. When we performed the $2-4$ reversal to change B from 2 to 4 , this broke the 1-4 chain. When we then performed the 2-3 reversal to change E from 3, this caused C to change from 3 to 2 . As a result, F remains connected to four different colors; this wasn’t reversed to three as expected.
Unfortunately, you can’t perform both reversals “at the same time” for the following reason. Let’s attempt to perform both reversals “at the same time.” In this crossed-chain diagram, when we swap 2 and 4 on B’s side of the 1-3 chain, one of the 4’s in the 1-4 chain may change into a 2, and when we swap 2 and 3 on E’s side of the 1-4 chain, one of the 3’s in the 1-3 chain may change into a 2 . This is shown in the following figure: one 2 in each chain is shaded gray. Recall that these figures are incomplete; they focus on one vertex (F), its neighbors (A thru E), and Kempe chains. Other vertices and edges are not shown.
Note how one of the 3’s changed into 2 on the left. This can happen when we reverse $\mathrm{C}$ and $\mathrm{E}$ (which were originally 3 and 2 ) on E’s side of the 1-4 chain. Note also how one of the 4’s changed into 2 on the right. This can happen when we reverse B and D (which were originally 2 and 4) outside of the 1-3 chain. Now we see where a problem can occur when attempting to swap the colors of two chains at the same time. If these two 2’s happen to be connected by an edge like the dashed edge shown above, if we perform the double reversal at the same time, this causes two vertices of the same color to share an edge, which isn’t allowed. We’ll revisit Kempe’s strategy for coloring a vertex with degree five in Chapter $25 .$
图论代考
数学代写|图论作业代写Graph Theory代考|The shading of one section of the B-R
由于 Kempe 链的每个部分都与同一颜色对的其他部分隔离,因此 Kempe 链的任何部分的颜色可以颠倒,但仍满足四色定理。这是一个重要且有用的概念。
上面 BR 链的一个部分的阴影说明了任何 Kempe 链的任何部分的颜色如何可以反转。请注意,我们反转了 BR 链的一个部分的颜色,但没有反转中心部分的颜色。同一条链的每个部分的颜色可以独立于该链的其他部分反转。
为什么 PG 有 Kempe 链?很容易理解为什么 MPG 有 Kempe 链。(由于 PG 是通过从 MPG 中去除边缘而形成的,并且由于适用于 MPG 的着色也适用于 PG,因此 PG 也具有 Kempe 链。)
- MPG 是三角测量的。它由具有三个边和三个顶点的面组成。
- 每个面的三个顶点必须是三种不同的颜色。
- 每条边由两个相邻的三角形共享,形成一个四边形。
- 每个四边形将有 3 或 4 种不同的颜色。如果与共享边相对的两个顶点恰好是相同的颜色,则它有 3 种颜色。
- 对于每个四边形,四个顶点中的至少 1 个顶点和最多 3 个顶点具有任何颜色对的颜色。例如,具有 R、G、B 和G有 1 个顶点R−是和3个顶点乙−G,或者您可以将其视为 1 个顶点乙−是和3个顶点G−R,或者您可以将其视为 BR 的 2 个顶点和 GY 的 2 个顶点。在后一种情况下,2G’ 不是同一链的连续颜色。
- 当您将更多三角形组合在一起(四边形仅组合两个)并考虑可能的颜色时,您将看到 Kempe 的部分
链子出现。我们将在 Chápter 中看到这些 Kémpé chảins 是如何出现的21.
也很容易看出一对颜色(如 RY)将如何与其对应颜色(BG)相邻:
- 画一张R顶点和一个是由边连接的顶点。
- 如果一个新顶点连接到这些顶点中的每一个,它必须是乙或者G.
- 如果一个新顶点连接到 R 而不是是,可能是是,乙, 或者G.
- 如果一个新的顶点连接到是但不是R,可能是R,乙, 或者G.
- RY 链要么继续增长,要么被 B 包围,G.
- 如果你关注 B 和 G,你会为它的链条得出类似的结论。
- 如果一条链条完全被其对应物包围,则链条的新部分可能会出现在其对应物的另一侧。
Kempe 证明了所有具有四阶的顶点(那些恰好连接到其他四个顶点的顶点)都是四色的 [Ref. 2]。例如,考虑下面的中心顶点。
数学代写|图论作业代写Graph Theory代考|In the previous figure
在上图中,顶点和是四度,因为它连接到其他四个顶点。Kempe 表明顶点 A、B、C 和 D 不能被强制为四种不同的颜色,这样顶点 E 总是可以被着色而不会违反四色定理,无论 MPG 的其余部分看起来如何上一页显示的部分。
- A 和 C 或者是 AC Kempe 链的同一部分的一部分,或者它们各自位于 AC Kempe 链的不同部分。(如果一种和C例如,是红色和黄色的,则 AC 链是红黄色链。) – 如果一种和C每个位于 AC Kempe 链的不同部分,其中一个部分的颜色可以反转,这有效地重新着色 C 以匹配 A 的颜色。如果 A 和 C 是 AC Kempe 链的同一部分的一部分,则 B 和 D每个都必须位于 BD Kempe 链的不同部分,因为 AC Kempe 链将阻止任何 BD Kempe 链从 B 到达 D。(如果乙和D是蓝色和绿色,例如,那么一种BD Kempe 链是蓝绿色链。)在这种情况下,由于 B 和 D 分别位于 BD Kempe 链的不同部分,因此 BD Kempe 链的其中一个部分的颜色可以反转,这有效地重新着色 D 以匹配 B颜色。– 因此,可以使 C 与 A 具有相同的颜色或使 D 具有与 A 相同的颜色乙通过反转 Kempe 链的分离部分。
上面的图表是不完整的。这些图只显示了一个四阶顶点(顶点 E)、它的最近邻居(A、B、C 和 D),以及 AC Kempe 链的片段。整个图还将包含几个其他顶点(特别是与 B 或 D 相同的颜色)和足够多的边以成为 MPG。左图有 A 连接到C在 AC Kempe 链的单个部分中(意味着该链的顶点颜色与 A 和 C 相同)。左图显示此 AC Kempe 链阻止 B 连接到DBD Kempe 链条的一个部分。中间的数字在 AC Kempe 链的不同部分有 A 和 C。在这种情况下,B 可以通过 BD Kempe 链的单个部分连接到 D。但是,由于四阶顶点的 A 和 C 位于不同的部分,因此可以反转 C 链的颜色,以便在四阶顶点中,C 有效地重新着色以匹配 A 的颜色,如右图所示. 类似地,可以在左图中反转 D 的部分,以便有效地重新着色 D 以匹配 B 的颜色。
Kempe 还试图证明五阶顶点是可四色的,以证明四色定理 [Ref. 2],但 Heawood 在 1890 年证明他关于五次顶点的论点是不充分的 [Ref. 3]。让我们探讨一下如果我们尝试将我们对度数为四的顶点的推理应用于度数为五的顶点会发生什么。
数学代写|图论作业代写Graph Theory代考|The previous diagrams
前面的图表显示,当在交叉链图中一次执行两种颜色反转时,第一次颜色反转可能会破坏另一个链,从而允许第二次颜色反转影响 F 的一个邻居的颜色。当我们执行2−4反转将 B 从 2 更改为 4 ,这打破了 1-4 链。然后,当我们执行 2-3 反转以将 E 从 3 更改时,这导致 C 从 3 更改为 2 。结果,F 仍然连接到四种不同的颜色;这并没有像预期的那样反转为三个。
不幸的是,由于以下原因,您不能“同时”执行两个冲销。让我们尝试“同时”执行两个反转。在这个交叉链图中,当我们在 1-3 链的 B 侧交换 2 和 4 时,1-4 链中的一个 4 可能会变成 2,当我们在 E 侧交换 2 和 3 时1-4 链,1-3 链中的 3 之一可能会变为 2 。如下图所示:每条链中的一个 2 为灰色阴影。回想一下,这些数字是不完整的;他们专注于一个顶点 (F)、它的邻居 (A 到 E) 和 Kempe 链。其他顶点和边未显示。
请注意左侧的 3 之一如何变为 2。当我们反转时会发生这种情况C和和(最初是 3 和 2 )在 1-4 链的 E 侧。还要注意 4 个中的一个如何在右侧变为 2。当我们在 1-3 链之外反转 B 和 D(最初是 2 和 4)时,就会发生这种情况。现在我们看到了尝试同时交换两条链的颜色时会出现问题的地方。如果这两个 2 恰好通过上图虚线这样的边连接起来,如果我们同时进行双重反转,就会导致两个相同颜色的顶点共享一条边,这是不允许的。我们将在第 1 章重新讨论 Kempe 为五阶顶点着色的策略25.
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。