如果你也在 怎样代写机器学习machine learning这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
机器学习是一种数据分析的方法,可以自动建立分析模型。它是人工智能的一个分支,其基础是系统可以从数据中学习,识别模式,并在最小的人为干预下做出决定。
statistics-lab™ 为您的留学生涯保驾护航 在代写机器学习machine learning方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写机器学习machine learning方面经验极为丰富,各种代写机器学习machine learning相关的作业也就用不着说。
我们提供的机器学习machine learning及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等楖率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
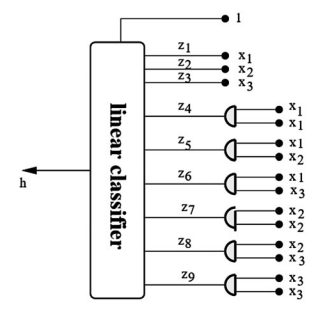
统计代写|机器学习作业代写machine learning代考|Polynomial Classifiers
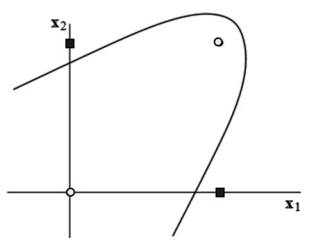
Let us now abandon the strict requirement that positive examples be linearly separable from negative ones. Quite often, they are not. Not only can the linear separability be destroyed by noise; the very shape of the region occupied by one of the classes can render linear decision surface inadequate. Thus in the training set shown in Fig. 4.5, no linear classifier ever succeeds in separating the two squares from the circles. Such separation can only be accomplished by a non-linear curve such as the parabola shown in the picture.
Non-linear Classifiers The point having been made, we have to ask how to induce these non-linear classifiers from data. To begin with, we have to decide what type of function to employ. This is not difficult. Math teaches us that any $n$ dimensional curve can be approximated to arbitrary precision with some polynomial of a sufficiently high order. Let us therefore take a look at how to induce from data these polynomials. Later, we will discuss their practical utility.
Polynomials of the Second Order The good news is that the coefficients of polynomials can be induced by the same techniques that we have used for linear classifiers. Let us explain how.
For the sake of clarity, we will begin by constraining ourselves to simple domains with only two Boolean attributes, $x_{1}$ and $x_{2}$. The second-order polynomial is then defined as follows:
$$
w_{0}+w_{1} x_{1}+w_{2} x_{2}+w_{3} x_{1}^{2}+w_{4} x_{1} x_{2}+w_{5} x_{2}^{2}=0
$$
The expression on the left is a sum of terms that have one thing in common: a weight, $w_{i}$, multiplies a product $x_{1}^{k} x_{2}^{l}$. In the first term, we have $k+l=0$, because $w_{0} x_{1}^{0} x_{2}^{0}=w_{0}$; next come the terms with $k+l=1$, concretely, $w_{1} x_{1}^{1} x_{2}^{0}=w_{1} x_{1}$ and $w_{2} x_{1}^{0} x_{2}^{1}=w_{1} x_{2}$; and the sequence ends with three terms that have $k+l=2$ : specifically, $w_{3} x_{1}^{2}, w_{4} x_{1}^{1} x_{2}^{1}$, and $w_{5} x_{2}^{2}$. The thing to remember is that the expansion of the second-order polynomial stops when the sum of the exponents reaches 2 .
Of course, some of the weights can be $w_{i}=0$, rendering the corresponding terms “invisible” such as in $7+2 x_{1} x_{2}+3 x_{2}^{2}$ where the coefficients of $x_{1}, x_{2}$, and $x_{1}^{2}$ are zero.
统计代写|机器学习作业代写machine learning代考|Specific Aspects of Polynomial Classifiers
Now that we understand that the main strength of polynomials is their almost unlimited flexibility, it is time to turn our attention to their shortcomings and limitations.
Overfitting Polynomial classifiers tend to overfit noisy training data. Since the problem of overfitting is typical of many machine-learning paradigms, it is a good idea discuss its essence in some detail. Let us constrain ourselves to twodimensional continuous domains that are easy to visualize.
The eight training examples in Fig. $4.7$ fall into two groups. In one group, all examples are positive (empty circles); in the other, all save one are negative (filled circles). Two attempts at separating the two classes are shown. The one on the left uses a linear classifier, ignoring the fact that one training example is thus misclassified. The one on the right resorts to a polynomial classifier in an attempt to avoid any error on the training set.
Inevitable Trade-Off Which of the two is to be preferred? The answer is not straightforward because we do not know the underlying nature of the data. It may be that the two classes are linearly separable, and the only cause for one positive example to be found in the negative region is class-label noise. If this is the case, the single error made by the linear classifier on the training set is inconsequential, whereas the polynomial on the right, cutting deep into the negative area, will misclassify those future examples that find themselves on the wrong side of the
curve. Conversely, it is possible that the outlier does represent some legitimate, even if rare, aspect of the positive class. In this event, the use of the polynomial is justified. Practically speaking, however, the assumption that the single outlier is only noise is more likely to be correct than the “special-aspect” alternative.
A realistic training set will contain not one, but quite a few, perhaps many examples that appear to be in the wrong area of the instance space. And the interclass boundary that the classifier seeks to approximate may indeed be curved, though how much curved is anybody’s guess. The engineer may regard the linear classifier as too crude, and opt instead for the more flexible polynomial. This said, a highorder polynomial will separate the two classes even in a very noisy training set-and then fail miserably on future data. The ideal solution is usually somewhere between the extremes and has to be determined experimentally.
统计代写|机器学习作业代写machine learning代考|Support Vector Machines
Now that we understand that polynomial classifiers do not call for any new learning algorithms, we can return to linear classifiers, a topic we have not yet exhausted. Let us abandon the restriction to the Boolean attributes, and consider also the possibility of the attributes being continuous. Can we then still rely on the two training algorithms described above?
Perceptron Learning in Numeric Domains In the case of perceptron learning, the answer is easy: yes, the same weight-modification formula can be used. Practical experience shows, however, that it is a good idea to normalize all attribute values so that they fall into the unit interval, $x_{i} \in[0,1]$. We can use to this end the normalization technique described in the chapter dealing with nearest-neighbor classifiers, in Sect. 3.3.
Let us repeat, for the reader’s convenience, the weight-adjusting formula:
$$
w_{i}=w_{i}+\eta[c(\mathbf{x})-h(\mathbf{x})] x_{i}
$$
Learning rate, $\eta$, and the difference between the real and hypothesized class labels, $[c(\mathbf{x})-h(\mathbf{x})]$, have the same meaning and impact as before. What has changed is the role of $x_{i}$. In the case of Boolean attributes, the value of $x_{i}=1$ or $x_{i}=0$ decided whether or not the corresponding weight should change. Here, however, the value of $x_{i}$ decides how much the weight should be affected: the change is greater if the attribute’s value is higher.
机器学习代写
统计代写|机器学习作业代写machine learning代考|Polynomial Classifiers
现在让我们放弃正样本与负样本线性可分的严格要求。很多时候,他们不是。不仅线性可分性会被噪声破坏;其中一类所占据的区域的形状可能会导致线性决策面不足。因此,在图 4.5 所示的训练集中,没有任何线性分类器能够成功地将两个正方形与圆形分开。这种分离只能通过非线性曲线来完成,例如图中所示的抛物线。
非线性分类器 已经提出了这一点,我们必须问如何从数据中归纳出这些非线性分类器。首先,我们必须决定使用什么类型的函数。这并不难。数学告诉我们,任何n尺寸曲线可以用一些足够高阶的多项式逼近到任意精度。因此,让我们看看如何从数据中导出这些多项式。稍后,我们将讨论它们的实际用途。
二阶多项式 好消息是多项式的系数可以通过我们用于线性分类器的相同技术来导出。让我们解释一下。
为了清楚起见,我们首先将自己限制在只有两个布尔属性的简单域中,X1和X2. 然后将二阶多项式定义如下:
在0+在1X1+在2X2+在3X12+在4X1X2+在5X22=0
左边的表达式是具有一个共同点的项的总和:权重,在一世, 乘积X1ķX2l. 在第一学期,我们有ķ+l=0, 因为在0X10X20=在0; 接下来是条款ķ+l=1, 具体来说,在1X11X20=在1X1和在2X10X21=在1X2; 并且该序列以三个具有的项结束ķ+l=2: 具体来说,在3X12,在4X11X21, 和在5X22. 要记住的是,当指数之和达到 2 时,二阶多项式的展开将停止。
当然,有些权重可以在一世=0,使相应的术语“不可见”,例如7+2X1X2+3X22其中的系数X1,X2, 和X12为零。
统计代写|机器学习作业代写machine learning代考|Specific Aspects of Polynomial Classifiers
既然我们了解多项式的主要优势在于它们几乎无限的灵活性,那么是时候将注意力转向它们的缺点和局限性了。
过拟合多项式分类器倾向于过拟合嘈杂的训练数据。由于过度拟合问题是许多机器学习范式的典型问题,因此最好详细讨论其本质。让我们将自己限制在易于可视化的二维连续域中。
图 8 中的 8 个训练样例。4.7分为两组。在一组中,所有示例都是正面的(空心圆圈);另一方面,除了一个都是负数(实心圆圈)。显示了分离这两个类的两次尝试。左边的那个使用线性分类器,忽略了一个训练示例因此被错误分类的事实。右边的那个求助于多项式分类器,试图避免训练集上的任何错误。
不可避免的权衡 两者中的哪一个是首选?答案并不简单,因为我们不知道数据的基本性质。可能这两个类是线性可分的,在负区域中找到一个正样本的唯一原因是类标签噪声。如果是这种情况,线性分类器在训练集上产生的单个错误是无关紧要的,而右边的多项式深入到负区域,将错误分类那些发现自己在错误一侧的未来示例
曲线。相反,异常值可能确实代表了正类的一些合法的,即使是罕见的方面。在这种情况下,使用多项式是合理的。然而,实际上,单个异常值只是噪声的假设比“特殊方面”替代方案更可能是正确的。
一个真实的训练集不会包含一个,而是相当多,也许很多的例子似乎在实例空间的错误区域。并且分类器试图近似的类间边界可能确实是弯曲的,尽管任何人都猜测弯曲的程度。工程师可能认为线性分类器过于粗糙,而选择更灵活的多项式。这就是说,即使在非常嘈杂的训练集中,高阶多项式也会将这两个类分开——然后在未来的数据上惨遭失败。理想的解决方案通常介于两个极端之间,并且必须通过实验确定。
统计代写|机器学习作业代写machine learning代考|Support Vector Machines
现在我们知道多项式分类器不需要任何新的学习算法,我们可以回到线性分类器,这是一个我们还没有穷尽的话题。让我们放弃对布尔属性的限制,同时考虑属性连续的可能性。那么我们还可以依赖上面描述的两种训练算法吗?
数值域中的感知器学习在感知器学习的情况下,答案很简单:是的,可以使用相同的权重修正公式。然而,实践经验表明,将所有属性值归一化以使其落入单位区间是一个好主意,X一世∈[0,1]. 为此,我们可以使用第 3 节中处理最近邻分类器一章中描述的规范化技术。3.3.
为方便读者,让我们重复一下权重调整公式:
在一世=在一世+这[C(X)−H(X)]X一世
学习率,这,以及真实和假设的类标签之间的差异,[C(X)−H(X)], 与以前的含义和影响相同。改变的是角色X一世. 在布尔属性的情况下,值X一世=1或者X一世=0决定相应的权重是否应该改变。然而,这里的价值X一世决定权重应该受到多大的影响:如果属性的值越高,变化越大。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。统计代写|python代写代考
随机过程代考
在概率论概念中,随机过程是随机变量的集合。 若一随机系统的样本点是随机函数,则称此函数为样本函数,这一随机系统全部样本函数的集合是一个随机过程。 实际应用中,样本函数的一般定义在时间域或者空间域。 随机过程的实例如股票和汇率的波动、语音信号、视频信号、体温的变化,随机运动如布朗运动、随机徘徊等等。
贝叶斯方法代考
贝叶斯统计概念及数据分析表示使用概率陈述回答有关未知参数的研究问题以及统计范式。后验分布包括关于参数的先验分布,和基于观测数据提供关于参数的信息似然模型。根据选择的先验分布和似然模型,后验分布可以解析或近似,例如,马尔科夫链蒙特卡罗 (MCMC) 方法之一。贝叶斯统计概念及数据分析使用后验分布来形成模型参数的各种摘要,包括点估计,如后验平均值、中位数、百分位数和称为可信区间的区间估计。此外,所有关于模型参数的统计检验都可以表示为基于估计后验分布的概率报表。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
statistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
机器学习代写
随着AI的大潮到来,Machine Learning逐渐成为一个新的学习热点。同时与传统CS相比,Machine Learning在其他领域也有着广泛的应用,因此这门学科成为不仅折磨CS专业同学的“小恶魔”,也是折磨生物、化学、统计等其他学科留学生的“大魔王”。学习Machine learning的一大绊脚石在于使用语言众多,跨学科范围广,所以学习起来尤其困难。但是不管你在学习Machine Learning时遇到任何难题,StudyGate专业导师团队都能为你轻松解决。
多元统计分析代考
基础数据: $N$ 个样本, $P$ 个变量数的单样本,组成的横列的数据表
变量定性: 分类和顺序;变量定量:数值
数学公式的角度分为: 因变量与自变量
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
