如果你也在 怎样代写监督学习Supervised and Unsupervised learning这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
监督学习算法从标记的训练数据中学习,帮你预测不可预见的数据的结果。成功地建立、扩展和部署准确的监督机器学习数据科学模型需要时间和高技能数据科学家团队的技术专长。此外,数据科学家必须重建模型,以确保给出的见解保持真实,直到其数据发生变化。
statistics-lab™ 为您的留学生涯保驾护航 在代写监督学习Supervised and Unsupervised learning方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写监督学习Supervised and Unsupervised learning代写方面经验极为丰富,各种代写监督学习Supervised and Unsupervised learning相关的作业也就用不着说。
我们提供的监督学习Supervised and Unsupervised learning及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
机器学习代写|监督学习代考Supervised and Unsupervised learning代写|Regression – An Introduction
This is an introductory chapter on the supervised (machine) learning from empirical data (i.e., examples, samples, measurements, records, patterns or observations) by applying support support vector machines (SVMs) a.k.a. kernel machines $^{1}$. The parts on the semi-supervised and unsupervised learning are given later and being entirely different tasks they use entirely different math and approaches. This will be shown shortly. Thus, the book introduces the problems gradually in an order of loosing the information about the desired output label. After the supervised algorithms, the semi-supervised ones will be presented followed by the unsupervised learning methods in Chap. 6 . The basic aim of this chapter is to give, as far as possible, a condensed (but systematic) presentation of a novel learning paradigm embodied in SVMs. Our focus will be on the constructive part of the SVMs’ learning algorithms for both the classification (pattern recognition) and regression (function approximation) problems. Consequently, we will not go into all the subtleties and details of the statistical learning theory (SLT) and structural risk minimization (SRM) which are theoretical foundations for the learning algorithms presented below. The approach here seems more appropriate for the application oriented readers. The theoretically minded and interested reader may find an extensive presentation of both the SLT and SRM in $[146,144,143,32,42,81,123]$. Instead of diving into a theory, a quadratic programming based learning, leading to parsimonious SVMs, will be presented in a gentle way – starting with linear separable problems, through the classification tasks having overlapped classes but still a linear separation boundary, beyond the linearity assumptions to the nonlinear separation boundary, and finally to the linear and nonlinear regression problems. Here, the adjective ‘parsimonious’ denotes a SVM with a small number of support vectors (‘hidden layer neurons’). The scarcity of the model results from a sophisticated, QP based, learning that matches the
model capacity to data complexity ensuring a good generalization, i.e., a good performance of SVM on the future, previously, during the training unseen, data.
Same as the neural networks (or similarly to them), SVMs possess the wellknown ability of being universal approximators of any multivariate function to any desired degree of accuracy. Consequently, they are of particular interest for modeling the unknown, or partially known, highly nonlinear, complex systems, plants or processes. Also, at the very beginning, and just to be sure what the whole chapter is about, we should state clearly when there is no need for an application of SVMs’ model-building techniques. In short, whenever there exists an analytical closed-form model (or it is possible to devise one) there is no need to resort to learning from empirical data by SVMs (or by any other type of a learning machine)
机器学习代写|监督学习代考Supervised and Unsupervised learning代写|Basics of Learning from Data
SVMs have been developed in the reverse order to the development of neural networks (NNs). SVMs evolved from the sound theory to the implementation and experiments, while the NNs followed more heuristic path, from applications and extensive experimentation to the theory. It is interesting to note that the very strong theoretical background of SVMs did not make them widely appreciated at the beginning. The publication of the first papers by Vapnik and Chervonenkis [145] went largely unnoticed till 1992 . This was due to a widespread belief in the statistical and/or machine learning community that, despite being theoretically appealing, SVMs are neither suitable nor relevant for practical applications. They were taken seriously only when excellent results on practical learning benchmarks were achieved (in numeral recognition, computer vision and text categorization). Today, SVMs show better results than (or comparable outcomes to) NNs and other statistical models, on the most popular benchmark problems.
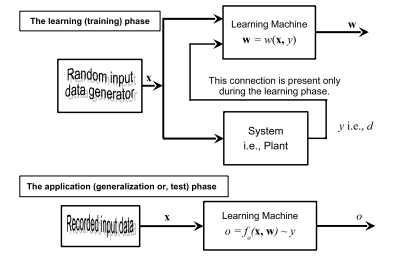
The learning problem setting for SVMs is as follows: there is some unknown and nonlinear dependency (mapping, function) $y=f(\mathbf{x})$ between some high-dimensional input vector $\mathbf{x}$ and the scalar output $y$ (or the vector output $\mathbf{y}$ as in the case of multiclass SVMs). There is no information about the underlying joint probability functions here. Thus, one must perform a distribution-free learning. The only information available is a training data set $\left{\mathcal{X}=[\mathbf{x}(i), y(i)] \in \mathfrak{R}^{m} \times \mathfrak{R}, i=1, \ldots, n\right}$, where $n$ stands for the number of the training data pairs and is therefore equal to the size of the training data set $\mathcal{X}$. Often, $y_{i}$ is denoted as $d_{i}$ (i.e., $t_{i}$ ), where $d(t)$ stands for a desired (target) value. Hence, SVMs belong to the supervised learning techniques.
Note that this problem is similar to the classic statistical inference. However, there are several very important differences between the approaches and assumptions in training SVMs and the ones in classic statistics and/or NNs
modeling. Classic statistical inference is based on the following three fundamental assumptions:
- Data can be modeled by a set of linear in parameter functions; this is a foundation of a parametric paradigm in learning from experimental data.
- In the most of real-life problems, a stochastic component of data is the normal probability distribution law, that is, the underlying joint probability distribution is a Gaussian distribution.
- Because of the second assumption, the induction paradigm for parameter estimation is the maximum likelihood method, which is reduced to the minimization of the sum-of-errors-squares cost function in most engineering applications.
All three assumptions on which the classic statistical paradigm relied turned out to be inappropriate for many contemporary real-life problems [143] because of the following facts:
- Modern problems are high-dimensional, and if the underlying mapping is not very smooth the linear paradigm needs an exponentially increasing number of terms with an increasing dimensionality of the input space (an increasing number of independent variables). This is known as ‘the curse of dimensionality’.
- The underlying real-life data generation laws may typically be very far from the normal distribution and a model-builder must consider this difference in order to construct an effective learning algorithm.
- From the first two points it follows that the maximum likelihood estimator (and consequently the sum-of-error-squares cost function) should be replaced by a new induction paradigm that is uniformly better, in order to model non-Gaussian distributions.
机器学习代写|监督学习代考Supervised and Unsupervised learning代写|Support Vector Machines in Classification
Below, we focus on the algorithm for implementing the SRM induction principle on the given set of functions. It implements the strategy mentioned previously – it keeps the training error fixed and minimizes the confidence interval. We first consider a ‘simple’ example of linear decision rules (i.e., the separating functions will be hyperplanes) for binary classification (dichotomization) of linearly separable data. In such a problem, we are able to perfectly classify data pairs, meaning that an empirical risk can be set to zero. It is the easiest classification problem and yet an excellent introduction of all relevant and important ideas underlying the SLT, SRM and SVM.
Our presentation will gradually increase in complexity. It will begin with a Linear Maximal Margin Classifier for Linearly Separable Data where there is no sample overlapping. Afterwards, we will allow some degree of overlapping of training data pairs. However, we will still try to separate classes by using linear hyperplanes. This will lead to the Linear Soft Margin Classifier for Overlapping Classes. In problems when linear decision hyperplanes are no longer feasible, the mapping of an input space into the so-called feature space (that ‘corresponds’ to the HL in NN models) will take place resulting in the Nonlinear Classifier. Finally, in the subsection on Regression by SV Machines we introduce same approaches and techniques for solving regression (i.e., function approximation) problems.
监督学习代写
机器学习代写|监督学习代考Supervised and Unsupervised learning代写|Regression – An Introduction
这是关于通过应用支持支持向量机 (SVM) 又名内核机从经验数据(即示例、样本、测量、记录、模式或观察)中进行监督(机器)学习的介绍性章节1. 半监督和无监督学习的部分稍后给出,它们是完全不同的任务,它们使用完全不同的数学和方法。这将很快显示。因此,本书以丢失有关所需输出标签的信息的顺序逐步介绍了这些问题。在监督算法之后,将介绍半监督算法,然后是第 1 章中的无监督学习方法。6. 本章的基本目的是尽可能简明(但系统地)介绍一种体现在 SVM 中的新颖学习范式。我们的重点将放在支持向量机的学习算法的建设性部分,用于分类(模式识别)和回归(函数逼近)问题。最后,我们不会深入探讨统计学习理论 (SLT) 和结构风险最小化 (SRM) 的所有细节和细节,它们是下面介绍的学习算法的理论基础。这里的方法似乎更适合面向应用程序的读者。有理论头脑和感兴趣的读者可能会发现 SLT 和 SRM 的广泛介绍[146,144,143,32,42,81,123]. 不是深入研究理论,而是以一种温和的方式呈现基于二次规划的学习,导致简约的 SVM——从线性可分离问题开始,通过具有重叠类但仍然是线性分离边界的分类任务,超越线性假设到非线性分离边界,最后到线性和非线性回归问题。在这里,形容词“简约”表示具有少量支持向量(“隐藏层神经元”)的 SVM。模型的稀缺性源于复杂的、基于 QP 的学习,该学习与
模型对数据复杂性的能力确保了良好的泛化性,即 SVM 在未来、以前、在训练期间看不见的数据上的良好性能。
与神经网络相同(或与它们类似),SVM 具有众所周知的能力,即可以将任何多元函数作为通用逼近器,达到任何所需的准确度。因此,它们对于建模未知或部分已知的高度非线性、复杂的系统、工厂或过程特别感兴趣。此外,在开始时,为了确定整章的内容,我们应该明确说明何时不需要应用 SVM 的模型构建技术。简而言之,只要存在分析封闭式模型(或可以设计一个),就无需借助 SVM(或任何其他类型的学习机)从经验数据中学习
机器学习代写|监督学习代考Supervised and Unsupervised learning代写|Basics of Learning from Data
支持向量机的发展与神经网络 (NN) 的发展相反。支持向量机从健全的理论发展到实现和实验,而神经网络则遵循更多的启发式路径,从应用和广泛的实验到理论。有趣的是,SVM 非常强大的理论背景并没有让它们在一开始就得到广泛的认可。Vapnik 和 Chervonenkis [145] 发表的第一篇论文直到 1992 年才被广泛关注。这是由于统计和/或机器学习社区普遍认为,尽管 SVM 在理论上很有吸引力,但它既不适合也不适用于实际应用。只有在实际学习基准(在数字识别、计算机视觉和文本分类)。如今,在最流行的基准问题上,SVM 显示出比 NN 和其他统计模型更好的结果(或与之相当的结果)。
支持向量机的学习问题设置如下:存在一些未知的非线性依赖(映射、函数)是=F(X)在一些高维输入向量之间X和标量输出是(或向量输出是与多类 SVM 的情况一样)。这里没有关于潜在联合概率函数的信息。因此,必须执行无分布的学习。唯一可用的信息是训练数据集\left{\mathcal{X}=[\mathbf{x}(i), y(i)] \in \mathfrak{R}^{m} \times \mathfrak{R}, i=1, \ldots, n\右}\left{\mathcal{X}=[\mathbf{x}(i), y(i)] \in \mathfrak{R}^{m} \times \mathfrak{R}, i=1, \ldots, n\右}, 在哪里n代表训练数据对的数量,因此等于训练数据集的大小X. 经常,是一世表示为d一世(IE,吨一世), 在哪里d(吨)代表期望的(目标)值。因此,支持向量机属于监督学习技术。
请注意,此问题类似于经典的统计推断。然而,训练支持向量机的方法和假设与经典统计和/或神经网络中的方法和假设之间存在几个非常重要的区别
造型。经典的统计推断基于以下三个基本假设:
- 数据可以通过一组线性参数函数来建模;这是从实验数据中学习的参数范式的基础。
- 在现实生活中的大多数问题中,数据的随机分量是正态概率分布规律,即潜在的联合概率分布是高斯分布。
- 由于第二个假设,参数估计的归纳范式是最大似然法,在大多数工程应用中,它被简化为误差平方和成本函数的最小化。
由于以下事实,经典统计范式所依赖的所有三个假设都被证明不适用于许多当代现实生活问题 [143]:
- 现代问题是高维的,如果底层映射不是很平滑,则线性范式需要随着输入空间维数的增加(自变量数量的增加)呈指数增加的项数。这被称为“维度的诅咒”。
- 现实生活中的基本数据生成规律通常可能与正态分布相差甚远,模型构建者必须考虑这种差异才能构建有效的学习算法。
- 从前两点可以看出,为了模拟非高斯分布,最大似然估计量(以及因此误差平方和成本函数)应该被一种更好的新归纳范式代替。
机器学习代写|监督学习代考Supervised and Unsupervised learning代写|Support Vector Machines in Classification
下面,我们重点介绍在给定函数集上实现 SRM 归纳原理的算法。它实现了前面提到的策略——它保持训练误差固定并最小化置信区间。我们首先考虑线性可分数据的二元分类(二分法)的线性决策规则(即,分离函数将是超平面)的“简单”示例。在这样的问题中,我们能够完美地对数据对进行分类,这意味着可以将经验风险设置为零。这是最简单的分类问题,也是对 SLT、SRM 和 SVM 基础的所有相关和重要思想的出色介绍。
我们的演示文稿将逐渐增加复杂性。它将从没有样本重叠的线性可分数据的线性最大边距分类器开始。之后,我们将允许训练数据对有一定程度的重叠。但是,我们仍然会尝试使用线性超平面来分离类。这将导致重叠类的线性软边距分类器。在线性决策超平面不再可行的问题中,将输入空间映射到所谓的特征空间(与 NN 模型中的 HL“对应”)将发生,从而产生非线性分类器。最后,在关于 SV 机器回归的小节中,我们介绍了解决回归(即函数逼近)问题的相同方法和技术。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
