如果你也在 怎样代写统计力学Statistical mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
统计力学是一个数学框架,它将统计方法和概率理论应用于大型微观实体的集合。它不假设或假定任何自然法则,而是从这种集合体的行为来解释自然界的宏观行为。
statistics-lab™ 为您的留学生涯保驾护航 在代写统计力学Statistical mechanics方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在代写统计力学Statistical mechanics代写方面经验极为丰富,各种代写统计力学Statistical mechanics相关的作业也就用不着说。
我们提供的统计力学Statistical mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:
- Statistical Inference 统计推断
- Statistical Computing 统计计算
- Advanced Probability Theory 高等概率论
- Advanced Mathematical Statistics 高等数理统计学
- (Generalized) Linear Models 广义线性模型
- Statistical Machine Learning 统计机器学习
- Longitudinal Data Analysis 纵向数据分析
- Foundations of Data Science 数据科学基础
物理代写|统计力学代写Statistical mechanics代考|The Second Law
The second law of thermodynamics concerns the nonexistence of a perpetuum mobile. This has long been a contentious issue but it is based on one of the most obvious facts of everyday experience, namely that certain processes are irreversible. This means simply that they cannot be reversed in time. Thus, e.g. the breaking of a glass on the floor is an irreversible process because the reverse process: the spontaneous creation of a glass from pieces on the floor simply does not happen. Characteristic of a process like that is that an ordered structure is destroyed which cannot be recreated without “doing something” to the system. It makes sense, therefore, to postulate the existence of a measure for the order in the system. Traditionally, one has chosen to introduce a measure of disorder instead, which is called the entropy. The second law is then a formulation of the creation of entropy in processes where the system is undisturbed. The first precise formulation of the second law was given by Lord Kelvin and Clausius. Kelvin’s formulation reads as follows.
There exists no thermodynamic transformation of which the only result is to convert heat from a heat reservoir to work.
Clausius’ formulation is slightly different.
There exists no thermodynamic transformation of which the only result is the transfer of heat from a colder heat reservoir to a hotter heat reservoir.
Clausius deduced from these basic statements the existence of a function of state which can only increase if the system is thermally isolated. This is the entropy which we simply postulate to exist. We then show in chapter 5 that our formulation implies their original statements.
To formulate the law in its entirety we need the following observation:
All thermodynamic parameters can be divided into two categories, namely intensive and extensive parameters. Intensive parameters are thermodynamic parameters that are independent of the size of the system; extensive parameters are thermodynamic parameters that are directly proportional to the size of the system.
物理代写|统计力学代写Statistical mechanics代考|Thermal Engines and Refrigerators
Thermodynamics was developed in a study of the efficient operation of thermal engines, the steam engine in particular. It is still important for these applications, e.g. the car engine, refrigerators, and steam turbines in electricity plants. The principle of operation of a heat engine is pictured schematically in figure 5.1.
Heat is absorbed from a heat reservoir at temperature $T_{A}$. The engine $E$ converts part of this heat into useful work $W$ and rejects the surplus heat $Q_{B}$ to a second heat reservoir at temperature $T_{B}$. Clearly,
$$
W=Q_{A}-Q_{B}
$$
The efficiency of the engine is defined as
$$
\eta=\frac{W}{Q_{A}} .
$$
Obviously, $\eta \leqslant 1$, but the second law gives a more stringent bound on the efficiency. Indeed, since
$$
\Delta S=-\frac{Q_{A}}{T_{A}}+\frac{Q_{B}}{T_{B}} \geqslant 0
$$
we find
$$
\eta \leqslant 1-\frac{T_{B}}{T_{A}} \equiv \eta_{C}
$$
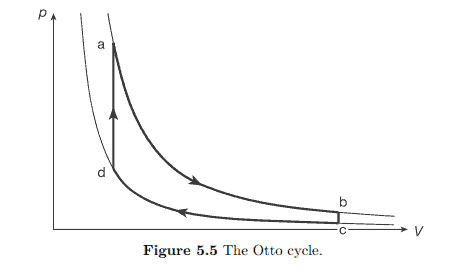
The maximum attainable efficiency $\eta_{C}$ is called the Carnot efficiency. It also follows that the most efficient engines are reversible, $\Delta S=0$. An example of a process in which the Carnot efficiency is attained is the Carnot process. For an ideal gas this process is represented by the cycle abcd in the following $p-V$ diagram of figure $5.2$.
$\mathrm{ab}$ and cd are isotherms, bc and da are adiabatics. In practice this process is very difficult to carry out. Most practical electricity plants use steam as working fluid. The process can then take place inside the coexistence region of steam and liquid water. This is called wet steam. It is then much easier to keep the temperature constant during the transfer of heat as the evaporation occurs at constant temperature. The process is most conveniently represented in a $T-s$ diagram (figure $5.3$ ).
In fact, the actual process used in practical power plants is considerably more complicated. Let us consider two of the most important modifications.
物理代写|统计力学代写Statistical mechanics代考|The Fundamental Equation
In this chapter, we show that the thermodynamics of a (simple) system is completely determined by a single function: the entropy density as a function of the internal energy density and the specific volume. This function has an important property, namely concavity, which enables us to define a number of other thermodynamic functions in chapter 8. Let us recall the definition of convex and concave functions: $A$ region $D$ in $\mathbb{R}^{k}$ is called convex if for every
two points $\vec{x}, \vec{y} \in D$ and every $t \in[0,1]$, also $t \vec{x}+(1-t) \vec{y} \in D$. A function $g: D \rightarrow \mathbb{R} \cup{+\infty}$ from a convex region $D \subset \mathbb{R}^{k}$ to the real line united with $+\infty$ is called convex if, for every $t \in[0,1]$ and all $\vec{x}, \vec{y} \in D$,
$$
g(t \vec{x}+(1-t) \vec{y}) \leqslant \operatorname{tg}(\vec{x})+(1-t) g(\vec{y})
$$
$g$ is called concave if $-g$ is convex. A region $D$ is convex when it does not have dents. Figures $6.1$ (a) and $6.1$ (b) show a convex region and a non-convex region respectively.
Similarly, a function is convex if its graph is everywhere bending upwards. In chapter 7 , we state and prove various useful facts about convex functions. Here, we first outline the significance for thermodynamic functions.
In the introduction and also in chapter 4 we remarked that, in order to describe a macroscopic system mathematically we have to take the thermodynamic limit, i.e. the limit of an infinitely large system with a finite particle number density: $N \rightarrow \infty, V \rightarrow \infty ; \quad \rho=N / V$ fixed. We also write $v=1 / \rho$ for the specific volume. In this limit all surface effects disappear and we are left with the pure bulk properties of the system. For intensive parameters $X(N, V, T)$ we expect the limit
$$
\lim {N, V \rightarrow \infty ; V / N=v} X(N, V, T)=x(v, T) $$ to exist, while for extensive variables $Y(N, V, T)$ we expect the limit $$ \lim {N, V \rightarrow \infty ; V / N=v} \frac{Y(N, V, T)}{N}=y(v, T)
$$
to exist. In other words, $X(N, V, T)=x(v, T)+o(1)$ and $Y(N, V, T)=$ $N y(v, T)+o(N)$ as $N \rightarrow \infty$. In fact, in real systems the values of $X$ and $Y / N$ fluctuate around their mean values $x(v, T)$ and $y(v, T)$.
Let us now concentrate in particular on the entropy density for a simple system defined by
$$
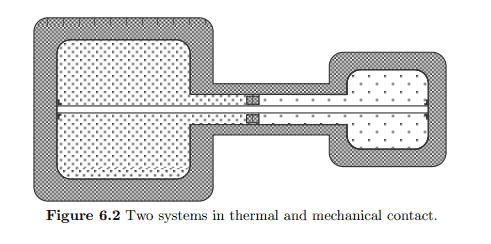
s(u, v)=\lim {N, V \rightarrow \infty ; V / N=v} \frac{1}{N} S(N u, V, N) $$ We shall argue that this function is concave in both its arguments. To show this we consider two systems $\Sigma{1}$ with parameters $\left(U_{1}, V_{1}, N_{1}\right)$ and $\Sigma_{2}$ with parameters $\left(U_{2}, V_{2}, N_{2}\right)$, which are brought into thermal and mechanical contact so that they can exchange energy and their relative volumes ean adjust. Figure $6.2$ gives an impression of this situation.
统计力学代考
物理代写|统计力学代写Statistical mechanics代考|The Second Law
热力学第二定律与永动机的不存在有关。这一直是一个有争议的问题,但它基于日常经验中最明显的事实之一,即某些过程是不可逆的。这意味着它们不能及时逆转。因此,例如在地板上打碎玻璃是一个不可逆的过程,因为相反的过程:从地板上的碎片自发地产生玻璃根本不会发生。像这样的过程的特征是有序结构被破坏,如果不对系统“做某事”就无法重新创建。因此,假设系统中存在秩序度量是有道理的。传统上,人们选择引入一种无序度量,称为熵。然后,第二定律是在系统不受干扰的过程中创建熵的公式。第二定律的第一个精确表述是由开尔文勋爵和克劳修斯给出的。开尔文的公式如下。
不存在唯一的结果是将热量从储热器转换为功的热力学转换。
克劳修斯的表述略有不同。
不存在唯一的结果是将热量从较冷的储热器转移到较热的储热器的热力学转换。
克劳修斯从这些基本陈述中推断出状态函数的存在,该函数只有在系统热隔离时才会增加。这是我们简单假设存在的熵。然后我们在第 5 章中表明,我们的表述暗示了它们的原始陈述。
为了完整地制定法律,我们需要以下观察:
所有的热力学参数都可以分为两类,即密集参数和扩展参数。密集参数是与系统大小无关的热力学参数;扩展参数是与系统大小成正比的热力学参数。
物理代写|统计力学代写Statistical mechanics代考|Thermal Engines and Refrigerators
热力学是在研究热机,特别是蒸汽机的有效运行时发展起来的。对于这些应用,例如汽车发动机、冰箱和发电厂中的蒸汽轮机,它仍然很重要。热机的工作原理如图 5.1 所示。
在一定温度下从储热器中吸收热量吨一个. 引擎和将部分热量转化为有用功在并排出多余的热量问乙到第二个热库在温度吨乙. 清楚地,
在=问一个−问乙
发动机的效率定义为
这=在问一个.
明显地,这⩽1,但第二定律对效率给出了更严格的限制。确实,自从
Δ小号=−问一个吨一个+问乙吨乙⩾0
我们发现
这⩽1−吨乙吨一个≡这C
可达到的最大效率这C称为卡诺效率。最有效的引擎也是可逆的,Δ小号=0. 获得卡诺效率的过程的一个例子是卡诺过程。对于理想气体,这个过程由下面的循环 abcd 表示p−在图形示意图5.2.
一个bcd 是等温线,bc 和 da 是绝热线。在实践中,这个过程很难进行。大多数实际的发电厂使用蒸汽作为工作流体。然后该过程可以在蒸汽和液态水的共存区域内进行。这称为湿蒸汽。由于蒸发发生在恒定温度下,因此在热传递过程中保持温度恒定会容易得多。该过程最方便地表示为吨−s图(图5.3 ).
事实上,实际发电厂中使用的实际过程要复杂得多。让我们考虑两个最重要的修改。
物理代写|统计力学代写Statistical mechanics代考|The Fundamental Equation
在本章中,我们展示了(简单)系统的热力学完全由一个函数决定:熵密度是内能密度和比容的函数。这个函数有一个重要的性质,即凹性,它使我们能够在第 8 章中定义许多其他热力学函数。让我们回顾一下凸函数和凹函数的定义:一个地区D在Rķ被称为凸如果对于每
两个点X→,是→∈D和每一个吨∈[0,1], 还吨X→+(1−吨)是→∈D. 一个函数G:D→R∪+∞从凸区域D⊂Rķ到实线联合+∞称为凸如果,对于每个吨∈[0,1]和所有X→,是→∈D,
G(吨X→+(1−吨)是→)⩽tg(X→)+(1−吨)G(是→)
G称为凹如果−G是凸的。一个地区D没有凹痕时是凸的。数字6.1(a) 和6.1(b) 分别表示凸区域和非凸区域。
类似地,如果函数的图形处处向上弯曲,则该函数是凸函数。在第 7 章中,我们陈述并证明了关于凸函数的各种有用事实。在这里,我们首先概述热力学函数的重要性。
在引言和第 4 章中,我们指出,为了在数学上描述宏观系统,我们必须采用热力学极限,即具有有限粒子数密度的无限大系统的极限:ñ→∞,在→∞;ρ=ñ/在固定的。我们也写在=1/ρ对于特定的音量。在这个极限内,所有的表面效应都消失了,我们只剩下系统的纯体积特性。对于密集参数X(ñ,在,吨)我们期望极限
林ñ,在→∞;在/ñ=在X(ñ,在,吨)=X(在,吨)存在,而对于广泛的变量是(ñ,在,吨)我们期望极限
林ñ,在→∞;在/ñ=在是(ñ,在,吨)ñ=是(在,吨)
存在。换句话说,X(ñ,在,吨)=X(在,吨)+○(1)和是(ñ,在,吨)= ñ是(在,吨)+○(ñ)作为ñ→∞. 事实上,在实际系统中,X和是/ñ围绕它们的平均值波动X(在,吨)和是(在,吨).
现在让我们特别关注由下式定义的简单系统的熵密度
s(在,在)=林ñ,在→∞;在/ñ=在1ñ小号(ñ在,在,ñ)我们将论证这个函数在它的两个参数中都是凹的。为了证明这一点,我们考虑两个系统Σ1带参数(在1,在1,ñ1)和Σ2带参数(在2,在2,ñ2),它们被带入热和机械接触,以便它们可以交换能量并且它们的相对体积可以调整。数字6.2给人这种情况的印象。
统计代写请认准statistics-lab™. statistics-lab™为您的留学生涯保驾护航。
金融工程代写
金融工程是使用数学技术来解决金融问题。金融工程使用计算机科学、统计学、经济学和应用数学领域的工具和知识来解决当前的金融问题,以及设计新的和创新的金融产品。
非参数统计代写
非参数统计指的是一种统计方法,其中不假设数据来自于由少数参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
术语 广义线性模型(GLM)通常是指给定连续和/或分类预测因素的连续响应变量的常规线性回归模型。它包括多元线性回归,以及方差分析和方差分析(仅含固定效应)。
有限元方法代写
有限元方法(FEM)是一种流行的方法,用于数值解决工程和数学建模中出现的微分方程。典型的问题领域包括结构分析、传热、流体流动、质量运输和电磁势等传统领域。
有限元是一种通用的数值方法,用于解决两个或三个空间变量的偏微分方程(即一些边界值问题)。为了解决一个问题,有限元将一个大系统细分为更小、更简单的部分,称为有限元。这是通过在空间维度上的特定空间离散化来实现的,它是通过构建对象的网格来实现的:用于求解的数值域,它有有限数量的点。边界值问题的有限元方法表述最终导致一个代数方程组。该方法在域上对未知函数进行逼近。[1] 然后将模拟这些有限元的简单方程组合成一个更大的方程系统,以模拟整个问题。然后,有限元通过变化微积分使相关的误差函数最小化来逼近一个解决方案。
tatistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
随机分析代写
随机微积分是数学的一个分支,对随机过程进行操作。它允许为随机过程的积分定义一个关于随机过程的一致的积分理论。这个领域是由日本数学家伊藤清在第二次世界大战期间创建并开始的。
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。
